Question

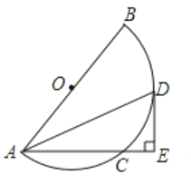
【题目】如图，在△ABC中，∠C＝90°，AC＝8 cm，BC＝6 cm.动点P在线段AC上以5 cm/s的速度从点A运动到点C.过点P作PD⊥AB于点D，以PD为一边向右作矩形PDEF，并且使DE＝AD.设点P的运动时间为t s，矩形PDEF和△ABC重叠部分图形周长为y cm．

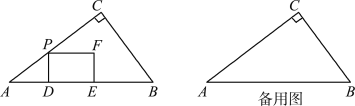
(1)当点F落在边BC上时，求t的值；

(2)求y与t之间的函数关系式；

(3)当矩形PDEF的面积被线段BC平分时，t＝______．

Answer 1

【答案】(1) t＝；(2)①y＝14t；②y＝t＋；③y＝－t＋20；(3) ．

【解析】

（1）如图1，由题意得出AB＝10、AP＝5t、PC＝85t，利用△APD∽△ABC求得AD＝4t、PD＝3t，据此知PF＝DE＝AD＝4t，由△CPF∽△CAB得，据此可得答案；

（2）分0＜t≤，＜t≤和≤t≤这三种情况，利用相似三角形的判定与性质求出重合部分图形的各边长度，从而得解；

（3）根据（1）、（2）所求结果，表示出四边形PDEF的面积为PDDE＝12t2、梯形PMBD的面积为(PM＋BD)·PD＝×[(8－5t)＋10－4t]×3t，，根据题意列出方程，解之可得．

（1）如图1，当点F落在BC上时，

∵AC＝8 cm，BC＝6 cm，∠C＝90°，

∴AB＝10cm，

由题意知，AP＝5t，

∵四边形PDEF为矩形，

∴∠PDA＝∠C＝90°，PF∥AB，PF＝DE，

∵∠A＝∠A，

∴△APD∽△ABC，

∴＝＝，即＝＝，则AD＝4t，PD＝3t，

∴PC＝AC－AP＝8－5t，PF＝DE＝AD＝4t，

∵PF∥AB，

∴△CPF∽△CAB，

∴，即，

解得t＝；

（2）①如图2，当0＜t≤时，

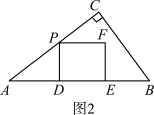
由(1)知，PD＝EF＝3t，PF＝DE＝4t，则y＝2(3t＋4t)＝14t；

②如图3，当＜t≤时，

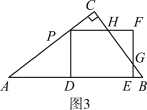
∵AP＝5t，AD＝DE＝4t，

∴PC＝8－5t，BE＝10－8t，

由△CPH∽△CAB知，，即，

解得PH＝(8－5t)，CH＝(8－5t)，

由△BEG∽△BCA知，，即，

解得EG＝(10－8t)，BG＝(10－8t)，

则HG＝BC－CH－BG＝6－(8－5t)－(10－8t)＝t－，

∴y＝3t＋4t＋(8－5t)＋t－＋(10－8t)＝t＋，

③如图4，当≤t≤时，

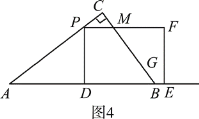
∵AP＝5t，AD＝DE＝4t，PD＝3t，

∴PC＝8－5t，BD＝AB－AD＝10－4t，

由②知，PM＝(8－5t)，CM＝(8－5t)，则BM＝BC－CM＝6－(8－5t)＝t，

∴y＝3t＋10－4t＋(8－5t)＋t＝－t＋20；

（3）如图4，

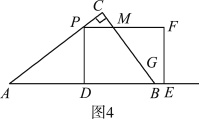
由(1)知，四边形PDEF的面积为PD·DE＝3t·4t＝12t2，

由(2)得梯形PMBD的面积为(PM＋BD)·PD＝×[(8－5t)＋10－4t]×3t，

∴根据题意得：×[(8－5t)＋10－4t]×3t＝×12t2，

解得t＝，

故答案为：．