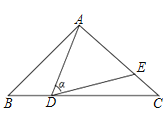
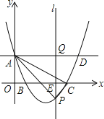
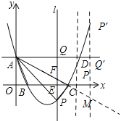
题目内容
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与
,与![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() ,且
,且![]() ,直线
,直线![]() 轴,在
轴,在![]() 轴上有一动点
轴上有一动点![]() 过点
过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() 与抛物线、直线
与抛物线、直线![]() 的交点分别为
的交点分别为![]() 、
、![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 当
当![]() 时,求
时,求![]() 面积的最大值;
面积的最大值;
![]() 当
当![]() 时,是否存在点
时,是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,求出此时
相似?若存在,求出此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() (2)12 (3)
(2)12 (3)![]() 或
或![]() 或
或![]()
【解析】
(1)认真审题,直接根据题意列出方程组,求出B,C两点的坐标,进而可求出抛物线的解析式;
(2)分0<t<6时和6<t≤8时两种情况进行讨论,据此即可求出三角形的最大值;
(3)以点D为分界点,分2<t≤8时和t>8时两种情况进行讨论,再根据三角形相似的条件,即可得解.
![]() 由题意知
由题意知![]() 、
、![]() 是方程
是方程![]() 的两根,
的两根,
∴![]() ,
,
由
解得: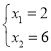
∴![]() 、
、![]()
则![]() ,
,
解得:![]() ,
,
∴该抛物线解析式为:![]() ;
;
![]() 可求得
可求得![]()
设直线![]() 的解析式为:
的解析式为:![]() ,
,
∵![]()
∴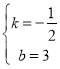
∴直线![]() 的解析式为:
的解析式为:![]() ,
,
要构成![]() ,显然
,显然![]() ,分两种情况讨论:
,分两种情况讨论:
①当![]() 时,设直线
时,设直线![]() 与
与![]() 交点为
交点为![]() ,则:
,则:![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
此时最大值为:![]() ,
,
②当![]() 时,设直线
时,设直线![]() 与
与![]() 交点为
交点为![]() ,则:
,则:![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
当![]() 时,取最大值,最大值为:
时,取最大值,最大值为:![]() ,
,
综上可知,当![]() 时,
时,![]() 面积的最大值为
面积的最大值为![]() ;
;
![]() 如图,连接
如图,连接![]() ,则
,则![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
①当![]() 时,
时,![]() ,
,![]() ,
,
若:![]() ,则:
,则:![]() ,
,
即: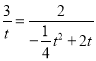 ,
,
∴![]() (舍),或
(舍),或![]() ,
,
若![]() ,则:
,则:![]() ,
,
即: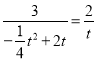 ,
,
∴![]() (舍)或
(舍)或![]() (舍),
(舍),
②当![]() 时,
时,![]() ,
,![]() ,
,
若:![]() ,则:
,则:![]() ,
,
即: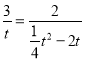 ,
,
∴![]() (舍),或
(舍),或![]() ,
,
若![]() ,则:
,则:![]() ,
,
即: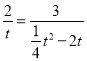 ,
,
∴![]() (舍)或
(舍)或![]() ,
,
∴![]() 或
或![]() 或
或![]() .
.

【题目】国家教育部提出“每天锻炼一小时,健康工作五十年,幸福生活一辈子”.万州区某中学对九年级部分学生进行问卷调查“你最喜欢的锻炼项目是什么?”,规定从“打球”,“跑步”,“游泳”,“跳绳”,“其他”五个选项中选择自己最喜欢的项目,且只能选择一个项目,并将调查结果绘制成如下两幅不完整的统计图.
最喜欢的锻炼项目 | 人数 |
打球 | 120 |
跑步 |
|
游泳 |
|
跳绳 | 30 |
其他 |
|
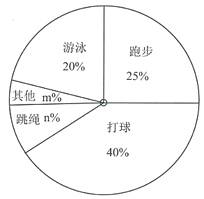
(1)这次问卷调查的学生总人数为 ,人数![]() ;
;
(2)扇形统计图中,![]() ,“其他”对应的扇形的圆心角的度数为 度;
,“其他”对应的扇形的圆心角的度数为 度;
(3)若该年级有1200名学生,估计喜欢“跳绳”项目的学生大约有多少人?