题目内容
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于A,B两点(点A在点B左侧)
轴交于A,B两点(点A在点B左侧)
(1)求抛物线的顶点坐标(用含![]() 的代数式表示);
的代数式表示);
(2)求线段AB的长;
(3)抛物线与![]() 轴交于点C(点C不与原点
轴交于点C(点C不与原点![]() 重合),若
重合),若![]() 的面积始终小于
的面积始终小于![]() 的面积,求
的面积,求![]() 的取值范围.
的取值范围.
【答案】(1)(2m,-1);(2)AB=2;(3)![]() <m<
<m<![]() 且m≠
且m≠![]() .
.
【解析】
(1)根据二次函数顶点坐标公式即可得答案;
(2)令y=0,可用m表示出A、B两点的横坐标,即可求出AB的值;
(3)由△OAC与△ABC等高且△OAC的面积始终小于△ABC的面积可知OA<AB,分点A在x轴正半轴和点A在x轴负半轴两种情况解答即可.
(1)∵抛物线的解析式为![]() ,
,
∴顶点坐标为[![]() ,
,![]() ],即(2m,-1).
],即(2m,-1).
(2)令y=0得:![]() =0,
=0,
解得:x1=2m-1,x2=2m+1,
∵点A在点B左侧,
∴A(2m-1,0),B(2m+1,0),
∴AB=2m+1-(2m-1)=2.
(3)∵△OAC与△ABC等高且△OAC的面积始终小于△ABC的面积,
∴OA<AB,
①当点A在x轴正半轴时,2m-1<2,
解得:m<![]() ,
,
②当点A在x轴负半轴时,-(2m-1)<2,
解得:m>![]() ,
,
∵点C不与原点![]() 重合,
重合,
∴4m2-1≠0,
解得:m≠±![]() ,
,
∴![]() <m<
<m<![]() 且m≠
且m≠![]() .
.

练习册系列答案
相关题目
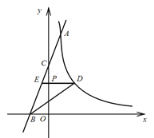
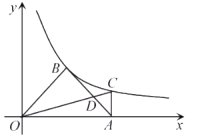
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图像交于点
的图像交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值和反比例函数的表达式;
的值和反比例函数的表达式;
(2)在![]() 轴上有一动点
轴上有一动点![]()
![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线,交反比例函数的图像于点
轴的直线,交反比例函数的图像于点![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,求
,求![]() 的值.
的值.