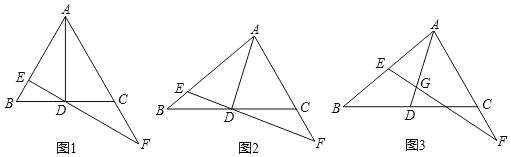
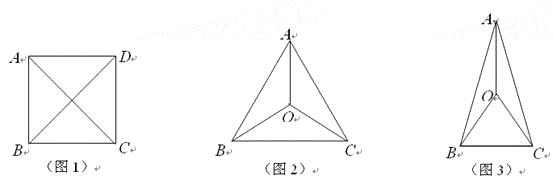
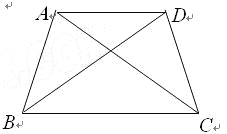
ЬтФПФкШн
ЁОЬтФПЁПдкЦНУцЩЯЃЌБпГЄЮЊ![]() ЕФе§ЗНаЮКЭЖЬБпГЄЮЊ
ЕФе§ЗНаЮКЭЖЬБпГЄЮЊ![]() ЕФОиаЮМИКЮжааФжиКЯЃЌШчЭМЂйЃЌЕБе§ЗНаЮКЭОиаЮЖМЫЎЦНЗХжУЪБЃЌШнвзЧѓГіжиЕўУцЛ§
ЕФОиаЮМИКЮжааФжиКЯЃЌШчЭМЂйЃЌЕБе§ЗНаЮКЭОиаЮЖМЫЎЦНЗХжУЪБЃЌШнвзЧѓГіжиЕўУцЛ§![]() ЃЎ
ЃЎ
МзЁЂввЁЂБћШ§ЮЛЭЌбЇЗжБ№ИјГіСЫСНИіЭМаЮВЛЭЌЕФжиЕўЗНЪНЃЛ
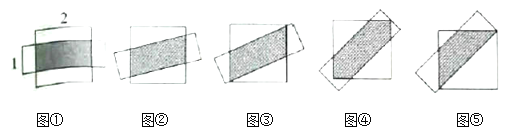
МзЃКОиаЮШЦзХМИКЮжааФа§зЊЃЌДгЭМЂкЕНЭМЂлЕФЙ§ГЬжаЃЌжиЕўУцЛ§![]() ДѓаЁВЛБфЃЎ
ДѓаЁВЛБфЃЎ
ввЃКШчЭМЂмЃЌОиаЮШЦзХМИКЮжааФМЬаја§зЊЃЌОиаЮЕФСНЬѕГЄБпгые§ЗНаЮЕФЖдНЧЯпЦНааЪБЃЌДЫЪБЕФжиЕўУцЛ§ДѓгкЭМЂлЕФжиЕўУцЛ§ЃЎ
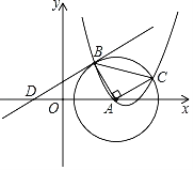
БћЃКШчЭМЂнЃЌНЋЭМЂмжаЕФОиаЮЯђзѓЩЯЗНЦНвЦЃЌЪЙОиаЮЕФвЛЬѕГЄБпЧЁКУОЙ§е§ЗНаЮЕФЖдНЧЯпЃЌДЫЪБЕФжиЕўУцЛ§ЪЧ![]() ИіЭМаЮжазюаЁЕФЃЎ
ИіЭМаЮжазюаЁЕФЃЎ
ЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ
A.МзЁЂввЁЂБћЖМЖдB.жЛгаввЖдC.жЛгаМзВЛЖдD.МзЁЂввЁЂБћЖМВЛЖд
ЁОД№АИЁПC
ЁОНтЮіЁП
БОЬтжиЕўВПЗжУцЛ§ашвЊНсКЯЭМаЮЬиЕуЃЌРћгУЖдГЦаджЪЃЌЭЈЙ§МйЩшЮДжЊЪ§БэЪОЮДжЊЯпЖЮЃЌРћгУУцЛ§ЙЋЪНЧѓНтЃЌВЂИљОнЯпЖЮЗЖЮЇХаБ№УцЛ§ДѓаЁЃЎ
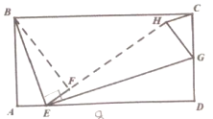
ШчЭМвЛЫљЪОЃЌЩшAI=xЃЌBJ=yЃЌдђгаx+y=AB-IJ=2-1=1ЃЌжиЕўВПЗжЫФБпаЮJILKУцЛ§ЮЊ2ЃЎ
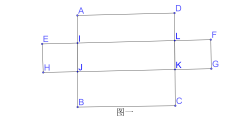
ШчЭМЖўЫљЪОЃЌЩшAI=xЃЌBJ=yЃЌ
вђЮЊJM=HE=1ЃЌЁїJIMЮЊжБНЧШ§НЧаЮЃЌаББпJIДѓгкжБНЧБпJMЃЌ
ЙЪгаЃКx+yЃМ1ЃЌжиЕўВПЗжЦНааЫФБпаЮJILKУцЛ§ЮЊ![]() ЃЎ
ЃЎ
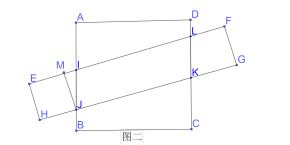
ШчЭМШ§ЫљЪОЃЌЩшAI=xЃЈ0ЃМxЃМ1ЃЉЃЌBJ=y=0ЃЌжиЕўВПЗжЫФБпаЮJIDKУцЛ§ЮЊ![]() ЃЎ
ЃЎ
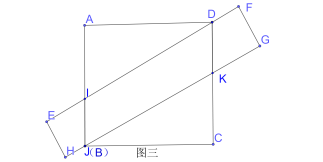
дкгЩЭМвЛЕНЭМШ§ЕФзЊБфЙ§ГЬжаЃЌx+yЕФШЁжЕж№НЅМѕаЁЃЌдђжиЕўВПЗжУцЛ§ж№НЅдіДѓЃЌЙЪМзЭЌбЇЫЕЗЈДэЮѓЃЎ
ШчЭМЫФЫљЪОЃЌЩшAI=AN=xЃЈ1ЃМxЃМ2ЃЉЃЌжиЕўВПЗжЖрБпаЮBINDKMУцЛ§ЮЊ![]() ЃЎ
ЃЎ
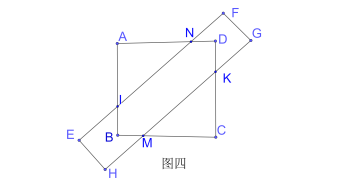
ЕБ0ЃМxЃМ2ЪБЃЌ![]() ЃЌЫљвдЭМЫФжиЕўВПЗжЕФУцЛ§ДѓгкЭМШ§жиЕўВПЗжУцЛ§ЃЌввЭЌбЇЫЕЗЈе§ШЗЃЎ
ЃЌЫљвдЭМЫФжиЕўВПЗжЕФУцЛ§ДѓгкЭМШ§жиЕўВПЗжУцЛ§ЃЌввЭЌбЇЫЕЗЈе§ШЗЃЎ
ШчЭМЮхЫљЪОЃЌЩшAI=AN=xЃЌЫљвджиЕўВПЗжЫФБпаЮINDBУцЛ§ЮЊ![]() ЃЌ
ЃЌ
вђЮЊ![]() ЃЌЫљвджиЕўВПЗжУцЛ§аЁгк2ЃЌМДаЁгкЭМвЛжиЕўУцЛ§ЃЎ
ЃЌЫљвджиЕўВПЗжУцЛ§аЁгк2ЃЌМДаЁгкЭМвЛжиЕўУцЛ§ЃЎ
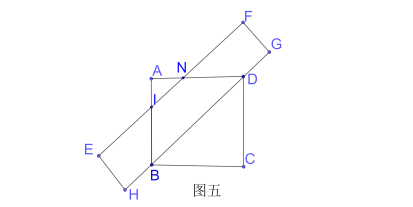
злЩЯЃЌЭМвЛЕНЭМЫФжиЕўВПЗжУцЛ§ж№НЅдіДѓЃЌЭМЮхУцЛ§аЁгкЭМвЛЃЌЙЪЭМЮхУцЛ§зюаЁЃЌБћЭЌбЇЫЕЗЈе§ШЗЃЎ
ЙЪД№АИЮЊCбЁЯюЃЎ

 ШЋгХЕуСЗЕЅдЊМЦЛЎЯЕСаД№АИ
ШЋгХЕуСЗЕЅдЊМЦЛЎЯЕСаД№АИ