题目内容
如图1,在平面直角坐标系中,以坐标原点O为圆心的⊙O的半径为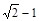 ,直线
,直线 与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M。
与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M。
(1)求点A的坐标及∠CAO的度数;
(2)⊙B以每秒1个单位长度的速度沿x轴负方向平移,同时,若直线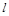 绕点A顺时针匀速旋转,当⊙B第一次与⊙O相切时,直线
绕点A顺时针匀速旋转,当⊙B第一次与⊙O相切时,直线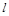 也恰好与⊙B第一次相切,见图(2)求B1的坐标以及直线AC绕点A每秒旋转多少度?
也恰好与⊙B第一次相切,见图(2)求B1的坐标以及直线AC绕点A每秒旋转多少度?
(3)若直线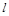 不动,⊙B沿x轴负方向平移过程中,能否与⊙O与直线
不动,⊙B沿x轴负方向平移过程中,能否与⊙O与直线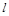 同时相切。若相切,说明理由。
同时相切。若相切,说明理由。
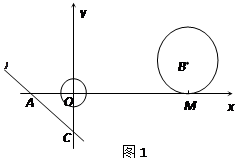
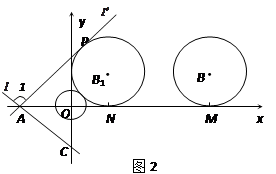
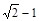 ,直线
,直线 与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M。
与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M。(1)求点A的坐标及∠CAO的度数;
(2)⊙B以每秒1个单位长度的速度沿x轴负方向平移,同时,若直线
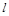 绕点A顺时针匀速旋转,当⊙B第一次与⊙O相切时,直线
绕点A顺时针匀速旋转,当⊙B第一次与⊙O相切时,直线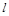 也恰好与⊙B第一次相切,见图(2)求B1的坐标以及直线AC绕点A每秒旋转多少度?
也恰好与⊙B第一次相切,见图(2)求B1的坐标以及直线AC绕点A每秒旋转多少度?(3)若直线
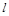 不动,⊙B沿x轴负方向平移过程中,能否与⊙O与直线
不动,⊙B沿x轴负方向平移过程中,能否与⊙O与直线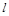 同时相切。若相切,说明理由。
同时相切。若相切,说明理由。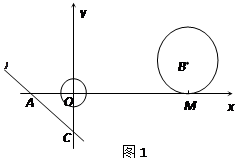
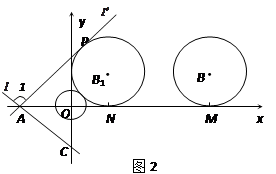
解: (1)A(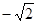 ,0)
,0)
∵ C(0,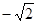 ). ∴ OA=OC ∵ OA⊥OC, ∴∠CAO=45°
). ∴ OA=OC ∵ OA⊥OC, ∴∠CAO=45°
(2) 如图,设⊙B平移t秒到⊙B1处与⊙O第一次相切,此时,直线l旋转到l1恰好与⊙B1 第一次相切于点P,⊙B1与x轴相切于点N,连接B1O,B1N.
则MN=t,O B1=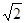 , B1N=1,B1N⊥AN.
, B1N=1,B1N⊥AN.
∴ON=1,∴MN=3,即t=3
连接B1A,B1P,则B1P⊥AP,B1P= B1N,∴∠PA B1="∠NA" B1.
∵OA="O" B1=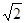 ,∴∠A B1O="∠NA" B1. ∴∠PA B1=∠A B1O. ∴PA∥B1O.
,∴∠A B1O="∠NA" B1. ∴∠PA B1=∠A B1O. ∴PA∥B1O.
在Rt△NO B1中,∠B1ON=45° ∴∠PAN=45° ∴∠1=90°.
∴直线AC绕点A平均每秒旋转30°
(3) 能,设⊙B与⊙O第二次相切时⊙B的圆心为B2,作B2E⊥AC于E,
作OH⊥AC于H,则四边形B2EHO为矩形,则B2E=OH=1,故此时⊙B与直线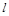 同时相切。
同时相切。
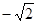 ,0)
,0)∵ C(0,
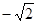 ). ∴ OA=OC ∵ OA⊥OC, ∴∠CAO=45°
). ∴ OA=OC ∵ OA⊥OC, ∴∠CAO=45° (2) 如图,设⊙B平移t秒到⊙B1处与⊙O第一次相切,此时,直线l旋转到l1恰好与⊙B1 第一次相切于点P,⊙B1与x轴相切于点N,连接B1O,B1N.
则MN=t,O B1=
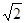 , B1N=1,B1N⊥AN.
, B1N=1,B1N⊥AN.∴ON=1,∴MN=3,即t=3
连接B1A,B1P,则B1P⊥AP,B1P= B1N,∴∠PA B1="∠NA" B1.
∵OA="O" B1=
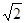 ,∴∠A B1O="∠NA" B1. ∴∠PA B1=∠A B1O. ∴PA∥B1O.
,∴∠A B1O="∠NA" B1. ∴∠PA B1=∠A B1O. ∴PA∥B1O.在Rt△NO B1中,∠B1ON=45° ∴∠PAN=45° ∴∠1=90°.
∴直线AC绕点A平均每秒旋转30°
(3) 能,设⊙B与⊙O第二次相切时⊙B的圆心为B2,作B2E⊥AC于E,
作OH⊥AC于H,则四边形B2EHO为矩形,则B2E=OH=1,故此时⊙B与直线
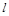 同时相切。
同时相切。(1)根据直线的解析式,易得AC的坐标,进而可得OA、OC的关系,由三角函数的定义可得∠CAO的大小;
(2)设相切时,MN=t,易得ON,MN的值,进而可得∠AB1O=∠NAB1,故PA∥B1O;易得在Rt△NOB1中,∠1=90°,即可得出答案;
(3)先假设能,且设⊙B与⊙O第二次相切时⊙B的圆心为B2,作B2E⊥AC于E.易得四边形B2EHO为平行四边形,此时⊙B与直线l同时相切.
(2)设相切时,MN=t,易得ON,MN的值,进而可得∠AB1O=∠NAB1,故PA∥B1O;易得在Rt△NOB1中,∠1=90°,即可得出答案;
(3)先假设能,且设⊙B与⊙O第二次相切时⊙B的圆心为B2,作B2E⊥AC于E.易得四边形B2EHO为平行四边形,此时⊙B与直线l同时相切.

练习册系列答案
相关题目
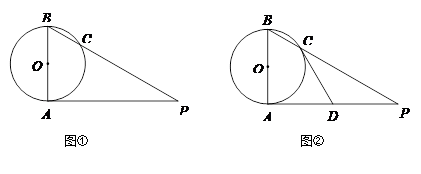
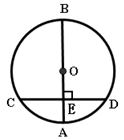
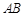 是⊙
是⊙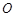 的直径,
的直径,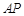 是⊙
是⊙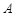 是切点,
是切点, 与⊙
与⊙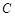 .
.
 ,
, ,求
,求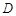 为
为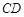 是⊙
是⊙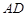 为
为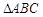 外接圆的直径,
外接圆的直径,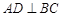 ,垂足为点
,垂足为点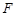 ,
,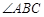 的平分线交
的平分线交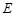 ,连接
,连接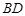 ,
,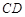 。
。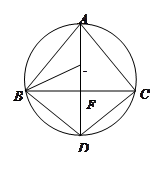
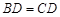 ;
; 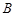 ,
,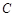 三点是否在以
三点是否在以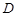 为圆心,以
为圆心,以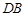 为半径的圆上?并说明理由。
为半径的圆上?并说明理由。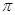 ,则这个圆锥的高为 .
,则这个圆锥的高为 .
 cm2的扇形纸片,现需要一个半径为
cm2的扇形纸片,现需要一个半径为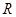 的圆形纸片,使两张纸片刚好能组合成圆锥体,则
的圆形纸片,使两张纸片刚好能组合成圆锥体,则
