题目内容
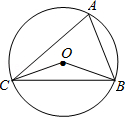
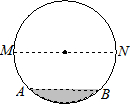
如图,圆O的直径AB的长为10,弦AC长为6,ÐACB的平分线交圆O于D,则CD长为

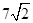
解:作DF⊥CA,垂足F在CA的延长线上,作DG⊥CB于点G,连接DA,DB.
∵CD平分∠ACB,
∴∠ACD=∠BCD
∴DF=DG,弧AD=弧BD,
∴DA=DB.
∵∠AFD=∠BGD=90°,
∴△AFD≌△BGD,
∴AF=BG.
易证△CDF≌△CDG,
∴CF=CG.
∵AC=6,BC=8,
∴AF=1,(也可以:设AF=BG=X,BC=8,AC=6,得8-X=6+X,解X=1)
∴CF=7,
∵△CDF是等腰直角三角形,(这里由CFDG是正方形也可得).
∴CD=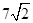 .
.
故选B.

∵CD平分∠ACB,
∴∠ACD=∠BCD
∴DF=DG,弧AD=弧BD,
∴DA=DB.
∵∠AFD=∠BGD=90°,
∴△AFD≌△BGD,
∴AF=BG.
易证△CDF≌△CDG,
∴CF=CG.
∵AC=6,BC=8,
∴AF=1,(也可以:设AF=BG=X,BC=8,AC=6,得8-X=6+X,解X=1)
∴CF=7,
∵△CDF是等腰直角三角形,(这里由CFDG是正方形也可得).
∴CD=
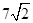 .
.故选B.

练习册系列答案
相关题目
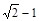 ,直线
,直线 与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M。
与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M。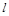 绕点A顺时针匀速旋转,当⊙B第一次与⊙O相切时,直线
绕点A顺时针匀速旋转,当⊙B第一次与⊙O相切时,直线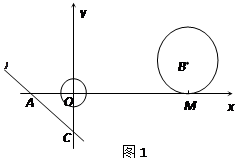
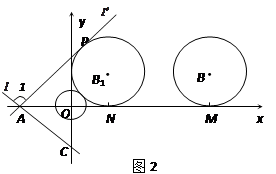


 B
B C8 D
C8 D
 的坐标为
的坐标为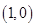 ,点
,点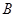 的坐标为
的坐标为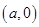 ,圆
,圆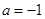 时,点
时,点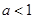 时,点
时,点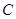 .当
.当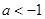 时,点
时,点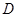 .当
.当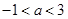 时,点
时,点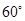 的圆心角所对的弦长为 .
的圆心角所对的弦长为 .