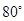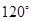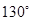题目内容
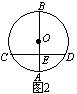
下图是输水管的切面，阴影部分是有水部分，其中水面宽16㎝，最深地方的高度是4㎝，求这个圆形切面的半径.
设圆形切面的半径，过点O作OD⊥AB于点D，交⊙O于点E，
则AD=BD=
AB=×16=8cm，
∵最深地方的高度是4cm，
∴OD=r=4，
在Rt△OBD中，
OB2=BD2+OD2，即r2=82+（r﹣4）2，
解得r=10（cm）．
答：这个圆形切面的半径是10cm．
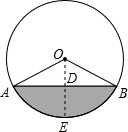
则AD=BD=
AB=×16=8cm，∵最深地方的高度是4cm，
∴OD=r=4，
在Rt△OBD中，
OB2=BD2+OD2，即r2=82+（r﹣4）2，
解得r=10（cm）．
答：这个圆形切面的半径是10cm．
设圆形切面的半径为r，过点O作OD⊥AB于点D，交⊙O于点E，由垂径定理可求出BD的长，再根据最深地方的高度是4cm得出OD的长，根据勾股定理即可求出OB的长．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
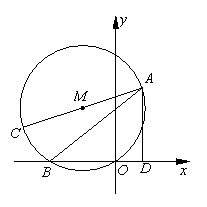
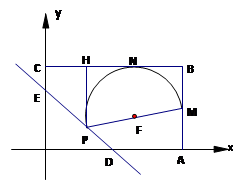
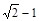，直线
与坐标轴分别交于A、C两点，点B的坐标为(4,1)，⊙B与x轴相切于点M。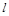
绕点A顺时针匀速旋转，当⊙B第一次与⊙O相切时，直线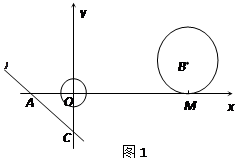
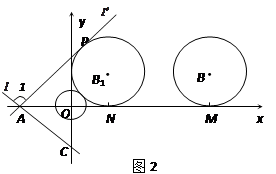
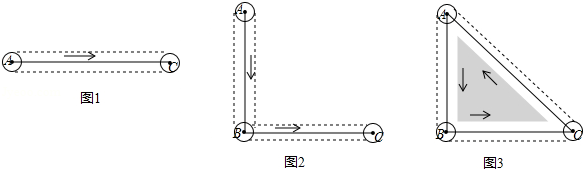
C方向运动到点C，求圆扫过的区域面积；
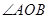的度数为
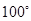，则圆周角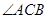
的度数是（ ）
