Question

【题目】在平面直角坐标系xOy中，抛物线与y轴交于点A，它的顶点为点B．

（1）点A的坐标为______，点B的坐标为______(用m表示)；

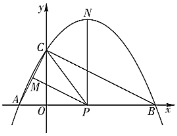
（2）已知点M(-6，4)，点N(3，4)，若抛物线与线段MN恰有一个公共点，结合函数图象，求m的取值范围．

Answer 1

【答案】（1）（0,1），（m，1-m）；（2）当m<-4，或m=-3或m>1时，抛物线与线段MN恰好有一个公共点

【解析】

（1）根据计算x=0即可得到点A的坐标，利用顶点坐标公式计算顶点坐标；

（2）根据题意画出函数图象，利用分类讨论的方法即可得到m的取值范围.

（1）当x=0时，得到y=1，∴点A的坐标是（0,1），

∵， ，

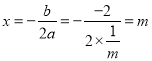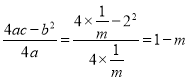∴顶点B的坐标是（m，1-m），

故答案为：（0,1），（m，1-m）；

（2）①当m<0时，

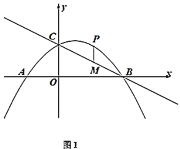
如图1：当m=-4时，抛物线与线段MN有两个公共点，且此时点M恰好在抛物线上，

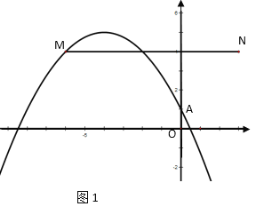
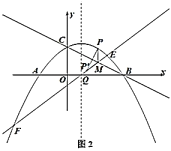
如图2：当m<-4时，此时点M在抛物线内，点N在抛物线外，抛物线与线段MN有一个交点，

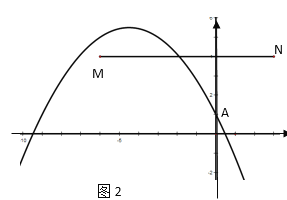
当-4<m<-3时，如图3，抛物线与线段MN有两个交点，

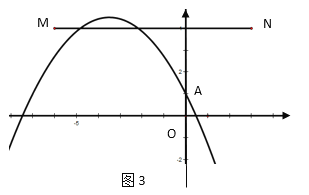
当m=-3时，如图4，抛物线与线段MN有一个交点，

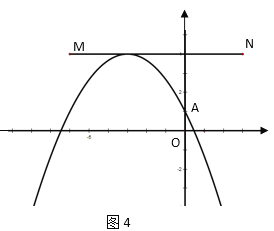
当-3<m<0时，抛物线与线段MN没有交点，

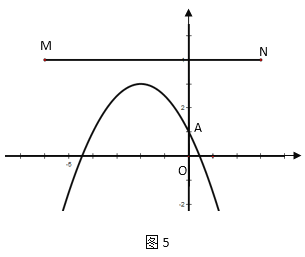
②当m>0时，

当0<m时，抛物线与线段MN有两个交点，

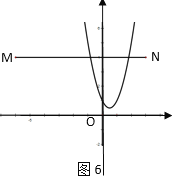
当m>1时，如图7，物线与线段MN有一个交点，

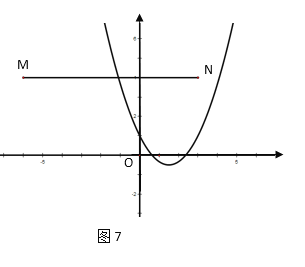
综上，当m<-4，或m=-3或m>1时，抛物线与线段MN恰好有一个公共点