Question

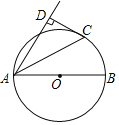
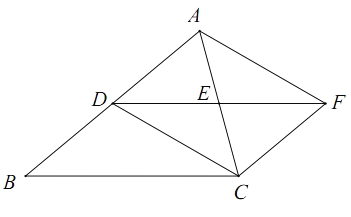
【题目】如图，在△ABC中，D为AB中点，过点D作DF//BC交AC于点E，且DE=EF，连接AF，CF，CD．

（1）求证：四边形ADCF为平行四边形；

（2）若∠ACD=45°，∠EDC=30°，BC=4，求CE的长．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）由DF∥BC，D为AB的中点得到AE=CE，再证明△AED≌△CEF推出AD=CF，AD∥CF，即可得到结论；

（2）作EM⊥CD于M，根据平行四边形的性质求出DF=4，得到DE=2，根据∠EDC=30°求出EM=1，再利用三角函数求出CE即可.

（1）∵DF∥BC，

∴,

∵D为AB的中点,

∴AE=CE，

∵DE=EF，∠AED=∠CEF，

∴△AED≌△CEF，

∴AD=CF，∠ADE=∠CFE，

∴AD∥CF，

∴四边形ADCF为平行四边形；

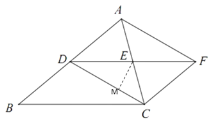
（2）作EM⊥CD于M，

∵四边形ADCF是平行四边形，BC=4，

∴DF=BC=4，

∴DE=2，

∵∠EDC=30°，

∴，

∵∠ACD=45°，

∴.