题目内容
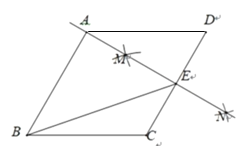
【题目】如图,在Rt△ABC中,∠C=90°(AC>BC),用尺规作图的方法作线段AD,保留作图痕迹如图所示,认真观察作图痕迹,若CD=4,BD=5,则AC的长为( )
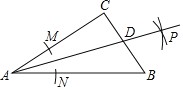
A.6B.9C.12D.15
【答案】C
【解析】
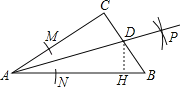
由作法得AD平分∠BAC,作DH⊥AB于D,如图,根据角平分线的性质得DH=DC=4,利用勾股定理计算出BH=3,再利用勾股定理得到AC=AH,设AC=x,则AB=x+2,则x2+92=(x+3)2,然后解方程即可.
解:由作法得AD平分∠BAC,
作DH⊥AB于D,如图,则DH=DC=4,
在Rt△BDH中,BH=3(勾股定理),
∵AC2=AD2﹣CD2,AH2=AD2﹣DH2,
∴AC=AH,
设AC=x,则AB=x+3,
在Rt△ABC中,x2+92=(x+3)2,解得x=12,
即AC的长为12.
故选:C.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目