题目内容
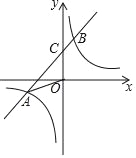
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象相交于点A(﹣3,﹣1)和点B,与y轴交于点C,△OAC的面积为3.
(m≠0)的图象相交于点A(﹣3,﹣1)和点B,与y轴交于点C,△OAC的面积为3.
(1)求反比例函数的解析式;
(2)求一次函数的解析式,并写出点B的坐标;
(3)连接BO并延长交双曲线的另一支于点E,将直线y=kx+b向下平移a (a>0)个单位长度后恰好经过点E,求a的值.
【答案】(1)y=![]() ;(2)y=x+2,B(1,3);(3)a=4.
;(2)y=x+2,B(1,3);(3)a=4.
【解析】
(1)利用待定系数法即可解决问题;
(2)利用三角形的面积公式求出点C坐标,再利用待定系数法求出直线的解析式,利用方程组确定解得B坐标即可;
(3)设直线y=x+2向下平移a(a>0)的单位,解析式为y=x+2-a,利用待定系数法即可解决问题.
(1)∵A(﹣3,﹣1)在y=![]() 上,
上,
∴m=3,
∴反比例函数的解析式为y=![]() .
.
(2)∵△OAC的面积为3.
∴![]() ×b×3=3,
×b×3=3,
∴b=2,
∵直线y=kx+b经过A(﹣3,﹣1),
∴﹣3k+2=﹣1,
∴k=1,
∴直线AB的解析式为y=x+2,
由 ,解得
,解得![]() 或
或![]() ,
,
∴B(1,3).
(3)根据对称性可知E(﹣1,﹣3),
设直线y=x+2向下平移a(a>0)的单位,解析式为y=x+2﹣a,
∵平移后经过(﹣1,﹣3),
∴﹣3=﹣1+2﹣a,
∴a=4.

练习册系列答案
相关题目