题目内容
【题目】如图,在等边三角形ABC的外侧作直线AP,点C关于直线AP的对称点为点D,连接AD,BD,其中BD交直线AP于点E.
(1)依题意补全图形;(2)若∠PAC=20°,求∠AEB的度数;
(3)连结CE,写出AE, BE, CE之间的数量关系,并证明你的结论.

【答案】(1)见解析;(2)60°;(3)CE +AE=BE,理由见解析
【解析】试题分析:(1)根据题意补全图形即可;(2)根据轴对称的性质可得AC=AD,∠PAC=∠PAD=20°,根据等边三角形的性质可得AC=AB,∠BAC=60°,即可得AB=AD,在△ABD 中,根据等腰三角形的性质和三角形的内角和定理求得∠D的度数,再由三角形外角的性质即可求得∠AEB的度数;(3)CE +AE=BE,如图,在BE上取点M使ME=AE,连接AM,设∠EAC=∠DAE=x,类比(2)的方法求得∠AEB=60°,从而得到△AME为等边三角形,根据等边三角形的性质和SAS即可判定△AEC≌△AMB,根据全等三角形的性质可得CE=BM,由此即可证得CE +AE=BE.
试题解析:
(1)如图:
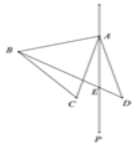
(2)在等边△ABC中,
AC=AB,∠BAC=60°
由对称可知:AC=AD,∠PAC=∠PAD,
∴AB=AD
∴∠ABD=∠D
∵∠PAC=20°
∴∠PAD=20°
∴∠BAD=∠BAC+∠PAC +∠PAD =100°
![]() .
.
∴∠AEB=∠D+∠PAD=60°
(3)CE +AE=BE.
在BE上取点M使ME=AE,连接AM,
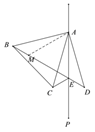
在等边△ABC中,
AC=AB,∠BAC=60°
由对称可知:AC=AD,∠EAC=∠EAD,
设∠EAC=∠DAE=x.
∵AD =AC=AB,
∴![]()
∴∠AEB=60-x+x =60°.
∴△AME为等边三角形.
∴AM=AE,∠MAE=60°,
∴∠BAC=∠MAE=60°,
即可得∠BAM=∠CAE.
在△AMB和△AEC中,
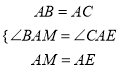 ,
,
∴△AMB≌△AEC.
∴CE=BM.
∴CE +AE=BE.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案




