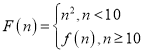题目内容
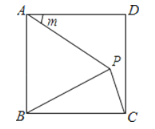
【题目】如图，在△ABC中，已知D，E分别为边BC，AD的中点，且S△ABC＝4 cm2，则△BEC的面积为( )
A. 2 cm2 B. 1 cm2 C. 0.5 cm2 D. 0.25 cm2
【答案】A
【解析】
首先根据E为AD的中点，可得BE、CE分别是△ABD、△ACD的中线，然后根据三角形的中线把三角形分成面积相同的两部分，可得S△BDE=
S△ABD，S△CDE=S△ACD，所以S△BEC= S△ABC，据此求出S△BEC的值为多少即可．
∵E为AD的中点，
∴BE、CE分别是△ABD、△ACD的中线，
∴S△BDE= S△ABD，S△CDE=S△ACD，
∴S△BEC= S△ABC=×4=2(cm2)，
即S△BEC的值为2 cm2.
故选：A.
练习册系列答案
相关题目
【题目】某超市计划购进甲、乙两种型号的台灯1000台，这两种型号台灯的进价、售价如下表：
进价（元/台） | 售价（元/台） | |
甲种 | 45 | 55 |
乙种 | 60 | 80 |
（1）如果超市的进货款为54000元，那么可计划购进甲、乙两种型号的台灯各多少台？
（2）为确保乙种型号的台灯销售更快，超市决定对乙种型号的台灯打折销售，且保证乙种型号台灯的利润率为
，问乙种型号台灯需打几折？
