题目内容
【题目】在平面直角坐标系xOy中,已知点A(0,8),点B(6,8),若点P同时满足下列条件:①点P到A,B两点的距离相等;②点P到∠xOy的两边距离相等.则点P的坐标为( ).

A.(3,5)B.(6,6)C.(3,3)D.(3,6)
【答案】C
【解析】
由点P到A、B两点的距离相等,故P在AB的中垂线上,再根据点P到∠xOy的两边距离相等,故点P在∠xOy的角平分线上,可在图中作出点P,然后根据A、B的坐标即可求出P点坐标.
解:∵点P到A,B两点的距离相等,点P到∠xOy的两边距离相等
∴点P在AB的中垂线上,也在∠xOy的角平分线上
∵点P即为AB的中垂线与∠xOy的角平分线的交点,如下图所示,点P即为所求
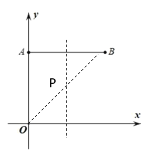
∵AB⊥y轴
∴AB的中垂线∥y轴
∴点P的横坐标与AB中点的横坐标相等,且AB中点横坐标为:![]()
∴P点横坐标为3
∵点P在∠xOy的角平分线上
∴P点横坐标=P点纵坐标=3
∴点P的坐标为(3,3)
故选C.

练习册系列答案
相关题目