ЬтФПФкШн
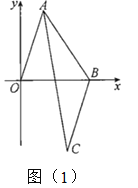
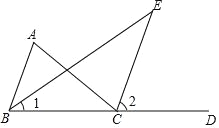
ЁОЬтФПЁПШчЭМЃЌвбжЊдкЁїABCжаЃЌCEЪЧЭтНЧЁЯACDЕФЦНЗжЯпЃЌBEЪЧЁЯABCЕФЦНЗжЯпЃЎ
(1)ЧѓжЄЃКЁЯAЃН2ЁЯEЃЌвдЯТЪЧаЁУїЕФжЄУїЙ§ГЬЃЌЧыдкРЈКХРяЬюаДРэгЩЃЎ
жЄУїЃКЁпЁЯACDЪЧЁїABCЕФвЛИіЭтНЧЃЌЁЯ2ЪЧЁїBCEЕФвЛИіЭтНЧЃЌ(вбжЊ)
ЁрЁЯACDЃНЁЯABC+ЁЯAЃЌЁЯ2ЃНЁЯ1+ЁЯE(_________)
ЁрЁЯAЃНЁЯACDЉЁЯABCЃЌЁЯEЃНЁЯ2ЉЁЯ1(ЕШЪНЕФаджЪ)
ЁпCEЪЧЭтНЧЁЯACDЕФЦНЗжЯпЃЌBEЪЧЁЯABCЕФЦНЗжЯп(вбжЊ)
ЁрЁЯACDЃН2ЁЯ2ЃЌЁЯABCЃН2ЁЯ1(_______)
ЁрЁЯAЃН2ЁЯ2Љ2ЁЯ1(_________)
ЃН2(ЁЯ2ЉЁЯ1)(_________)
ЃН2ЁЯE(ЕШСПДњЛЛ)
(2)ШчЙћЁЯAЃНЁЯABCЃЌЧѓжЄЃКCEЁЮABЃЎ
ЁОД№АИЁП(1)МћНтЮіЃЛ(2)жЄУїМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнНЧЦНЗжЯпЕФаджЪвдМАШ§НЧаЮЭтНЧЕФаджЪМДПЩЧѓжЄЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉПЩжЊЃКЁЯAЃН2ЁЯEЃЌгЩгкЁЯAЃНЁЯABCЃЌЁЯABCЃН2ЁЯABEЃЌЫљвдЁЯEЃНЁЯABEЃЌДгЖјПЩжЄABЁЮCEЃЎ
НтЃК(1)ЁпЁЯACDЪЧЁїABCЕФвЛИіЭтНЧЃЌЁЯ2ЪЧЁїBCEЕФвЛИіЭтНЧЃЌ(вбжЊ)ЃЌ
ЁрЁЯACDЃНЁЯABC+ЁЯAЃЌЁЯ2ЃНЁЯ1+ЁЯE(Ш§НЧаЮЭтНЧЕФаджЪ)ЃЌ
ЁрЁЯAЃНЁЯACDЉЁЯABCЃЌЁЯEЃНЁЯ2ЉЁЯ1(ЕШЪНЕФаджЪ)ЃЌ
ЁпCEЪЧЭтНЧЁЯACDЕФЦНЗжЯпЃЌBEЪЧЁЯABCЕФЦНЗжЯп(вбжЊ)ЃЌ
ЁрЁЯACDЃН2ЁЯ2ЃЌЁЯABCЃН2ЁЯ1(НЧЦНЗжЯпЕФаджЪ )ЃЌ
ЁрЁЯAЃН2ЁЯ2Љ2ЁЯ1( ЕШСПДњЛЛ)ЃЌ
ЃН2(ЁЯ2ЉЁЯ1)(ЬсШЁЙЋвђЪ§)ЃЌ
ЃН2ЁЯE(ЕШСПДњЛЛ)ЃЛ
(2)гЩ(1)ПЩжЊЃКЁЯAЃН2ЁЯE
ЁпЁЯAЃНЁЯABCЃЌЁЯABCЃН2ЁЯABEЃЌ
Ёр2ЁЯEЃН2ЁЯABEЃЌ
МДЁЯEЃНЁЯABEЃЌ
ЁрABЁЮCEЃЎ

 УћаЃСЊУЫПьРжПЮЬУЯЕСаД№АИ
УћаЃСЊУЫПьРжПЮЬУЯЕСаД№АИ