题目内容
【题目】如图，已知一次函数y =-x+7与正比例函数y=
x的图象交于点A，且与x轴交于点B．
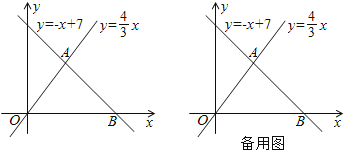
（1）求点A和点B的坐标；
（2）过点A作AC⊥y轴于点C，过点B作直线l∥y轴．动点P从点O出发，以每秒1个单位长的速度，沿O—C—A的路线向点A运动；同时直线l从点B出发，以相同速度向左平移，在平移过程中，直线l交x轴于点R，交线段BA或线段AO于点Q．当点P到达点A时，点P和直线l都停止运动．在运动过程中，设动点P运动的时间为t秒．
①当t为何值时，以A、P、R为顶点的三角形的面积为8？
②是否存在以A、P、Q为顶点的三角形是直角三角形？若存在，求t的值；若不存在，请说明理由．
【答案】（1） A（3，4）．B（7，0）．（2） 当t=2时，以A、P、R为顶点的三角形的面积为8．1或
．
【解析】
试题分析：（1）根据图象与坐标轴交点求法直接得出即可，再利用直线交点坐标求法将两直线解析式联立即可得出交点坐标；
（2）①利用S梯形ACOB-S△ACP-S△POR-S△ARB=8，表示出各部分的边长，整理出一元二次方程，求出即可；
②根据一次函数与坐标轴的交点得出，∠OBN=∠ONB=45°，进而利用勾股定理以及等腰三角形的性质和角三角形的判定求出即可．
试题解析：（1）根据题意，得
，解得
，
∴A（3，4） ．
令y=-x+7=0，得x=7．
∴B（7，0）．
（2）①当P在OC上运动时，0≤t＜4．
由S△APR=S梯形COBA-S△ACP-S△POR-S△ARB=8，得
（3+7）×4-×3×（4-t）- t（7-t）- t×4=8
整理,得t2-8t+12=0, 解之得t1=2,t2=6（舍）
当P在CA上运动，4≤t＜7．
由S△APR= ×（7-t） ×4=8，得t=3（舍）
∴当t=2时，以A、P、R为顶点的三角形的面积为8．
②当P在OC上运动时，0≤t＜4．
∠PAQ=90，t=1
当P在CA上运动时，4≤t＜7．
∠APQ=90, t=5．5 ∠AQP=90, t=
