ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌГЄЗНаЮABCDдкЦНУцжБНЧзјБъЯЕжаЃЌADЁЮBCЁЮxжсЃЌABЁЮDCЁЮyжсЃЌxжсгыyжсМаНЧЮЊ90ЁуЃЌЕуMЃЌNЗжБ№дкxyжсЩЯЃЌЕуAЃЈ1ЃЌ8ЃЉЃЌBЃЈ1ЃЌ6ЃЉЃЌCЃЈ7ЃЌ6ЃЉЃЌDЃЈ7ЃЌ8ЃЉЃЎ

ЃЈ1ЃЉСЌНгЯпЖЮOBЁЂODЁЂBDЃЌЧѓЁїOBDЕФУцЛ§ЃЛ
ЃЈ2ЃЉШєГЄЗНаЮABCDдкЕквЛЯѓЯоФквдУПУы0.5ИіЕЅЮЛГЄЖШЕФЫйЖШЯђЯТЦНвЦЃЌОЙ§ЖрЩйУыЪБЃЌЁїOBDЕФУцЛ§гыГЄЗНаЮABCDЕФУцЛ§ЯрЕШЧыжБНгаДГіД№АИЃЛ
ЃЈ3ЃЉМћБИгУЭМЃЌСЌНг OBЃЌODЃЌODНЛBCгкЕуEЃЌЁЯBONЕФЦНЗжЯпКЭЁЯBEOЕФЦНЗжЯпНЛгкЕуFЃЎ
ЂйЕБЁЯBEOЕФЖШЪ§ЮЊnЃЌЁЯBONЕФЖШЪ§ЮЊmЪБЃЌЧѓЁЯOFEЕФЖШЪ§ЃЎ
ЂкЧыжБНгаДГіЁЯOFEКЭЁЯBOEжЎМфЕФЪ§СПЙиЯЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ17ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉЂйЁЯEFOЃН
ЃЛЃЈ3ЃЉЂйЁЯEFOЃН![]() m+
m+![]() n+90ЁуЃЛЂк2ЁЯEFO+ЁЯBOEЃН270ЁуЃЎ
n+90ЁуЃЛЂк2ЁЯEFO+ЁЯBOEЃН270ЁуЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉбгГЄDAНЛyжсгкHЃЌШчЭМ1ЫљЪОЃЌдђAHЁЭyжсЃЌШЛКѓРћгУSЁїOBDЃНSЁїODHЉSЁїABDЉSЬнаЮAHOBДњШыЪ§ОнМЦЫуМДПЩЃЛ
ЃЈ2ЃЉгЩSЁїOBDЃНSЁїODHЉSЁїABDЉSЬнаЮAHOBЃНSГЄЗНаЮABCDЃН12МДПЩСаГіЙигкtЕФЗНГЬЃЌНтЗНГЬМДЕУНсЙћЃЛ
ЃЈ3ЃЉЂйбгГЄCBНЛyжсгкЕуPЃЌбгГЄEFНЛyжсгкЕуGЃЌШчЭМ2ЃЌИљОнНЧЦНЗжЯпЕФЖЈвхКЭШ§НЧаЮЕФЭтНЧаджЪНтД№МДПЩЃЛ
ЂкИљОнНЧЦНЗжЯпЕФЖЈвхКЭШ§НЧаЮЕФЭтНЧаджЪПЩЕУЁЯEFOЃН90Ёу+![]() (ЁЯNOB+ЁЯBEO)ЃЌИљОнжБНЧШ§НЧаЮЕФаджЪПЩЕУЁЯBON+ЁЯBEO=90ЁуЃЁЯBOEЃЌНјвЛВНМДПЩЕУГіНсТлЃЎ
(ЁЯNOB+ЁЯBEO)ЃЌИљОнжБНЧШ§НЧаЮЕФаджЪПЩЕУЁЯBON+ЁЯBEO=90ЁуЃЁЯBOEЃЌНјвЛВНМДПЩЕУГіНсТлЃЎ
НтЃКЃЈ1ЃЉбгГЄDAНЛyжсгкHЃЌШчЭМ1ЫљЪОЃК
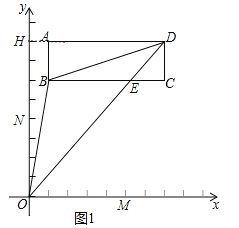
дђAHЁЭyжсЃЎ
ЁпAЃЈ1ЃЌ8ЃЉЃЌBЃЈ1ЃЌ6ЃЉЃЌCЃЈ7ЃЌ6ЃЉЃЌDЃЈ7ЃЌ8ЃЉ
ЁрOHЃН8ЃЌDHЃН7ЃЌAHЃН1ЃЌADЃН6ЃЌABЃН2ЃЌ
ЁрSЁїOBDЃНSЁїODHЉSЁїABDЉSЬнаЮAHOB
ЃН![]() ЁСOHЁСDHЉ
ЁСOHЁСDHЉ![]() ЁСABЁСADЉ
ЁСABЁСADЉ![]() ЁСЃЈAB+OHЃЉЁСAH
ЁСЃЈAB+OHЃЉЁСAH
ЃН![]() ЁС8ЁС7Љ
ЁС8ЁС7Љ![]() ЁС2ЁС6Љ
ЁС2ЁС6Љ![]() ЁСЃЈ2+8ЃЉЁС1ЃН17ЃЛ
ЁСЃЈ2+8ЃЉЁС1ЃН17ЃЛ
ЃЈ2ЃЉЁпSГЄЗНаЮABCDЃН2ЁС6ЃН12ЃЌ
ЁрSЁїOBDЃНSЁїODHЉSЁїABDЉSЬнаЮAHOBЃН12ЃЌ
Ёр![]() ЁСЃЈ8Љ0.5tЃЉЁС7Љ
ЁСЃЈ8Љ0.5tЃЉЁС7Љ![]() ЁС2ЁС6Љ
ЁС2ЁС6Љ![]() ЁСЃЈ2+8Љ0.5tЃЉЁС1ЃН12ЃЌ
ЁСЃЈ2+8Љ0.5tЃЉЁС1ЃН12ЃЌ
НтЕУЃКtЃН![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЂйбгГЄCBНЛyжсгкЕуPЃЌбгГЄEFНЛyжсгкЕуGЃЌШчЭМ2ЃЌ
ЁпEFЦНЗжЁЯBEOЃЌOFЦНЗжЁЯNOBЃЌ
ЁрЁЯGOFЃН![]() ЁЯNOBЃН
ЁЯNOBЃН![]() mЃЌЁЯBEFЃН
mЃЌЁЯBEFЃН![]() ЁЯBEOЃН
ЁЯBEOЃН![]() nЃЌ
nЃЌ
ЁпЁЯEFOЃНЁЯGOF+ЁЯFGOЃЌЁЯFGOЃНЁЯGPE+ЁЯBEFЃЌ
ЁрЁЯEFOЃНЁЯGOF+ЁЯGPE+ЁЯBEFЃН![]() m+
m+![]() n+90ЁуЃЛ
n+90ЁуЃЛ
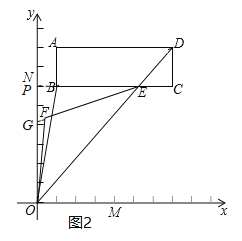
ЂкЁпEFЦНЗжЁЯBEOЃЌOFЦНЗжЁЯNOBЃЌ
ЁрЁЯGOFЃН![]() ЁЯNOBЃЌЁЯBEFЃН
ЁЯNOBЃЌЁЯBEFЃН![]() ЁЯBEOЃЌ
ЁЯBEOЃЌ
ЁпЁЯEFOЃНЁЯGOF+ЁЯFGOЃЌЁЯFGOЃНЁЯGPE+ЁЯBEFЃЌ
ЁрЁЯEFOЃНЁЯGOF+ЁЯGPE+ЁЯBEFЃН90Ёу+![]() ЁЯNOB+
ЁЯNOB+![]() ЁЯBEOЃН90Ёу+
ЁЯBEOЃН90Ёу+![]() (ЁЯNOB+ЁЯBEO)ЃЌ
(ЁЯNOB+ЁЯBEO)ЃЌ
ЁпЁЯBOEЃН90ЁуЉЁЯBONЉЁЯBEOЃЌ
ЁрЁЯBON+ЁЯBEO=90ЁуЃЁЯBOEЃЌ
ЁрЁЯEFOЃН90Ёу+![]() (90ЁуЃЁЯBOE)ЃЌ
(90ЁуЃЁЯBOE)ЃЌ
МД2ЁЯEFO+ЁЯBOEЃН270ЁуЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИЁОЬтФПЁПЮвЯиЭђЕТТЁЩЬГЁгаAЁЂBСНжжЩЬЦЗЕФНјМлКЭЪлМлШчБэЃК
ЩЬЦЗ МлИё | A | B |
НјМлЃЈдЊ/МўЃЉ | m | m+20 |
ЪлМлЃЈдЊ/МўЃЉ | 160 | 240 |
вбжЊЃКгУ2400дЊЙКНјAжжЩЬЦЗЕФЪ§СПгыгУ3000дЊЙКНјBжжЩЬЦЗЕФЪ§СПЯрЭЌЃЎ
ЃЈ1ЃЉЧѓmЕФжЕЃЛ
ЃЈ2ЃЉИУЩЬГЁМЦЛЎЭЌЪБЙКНјЕФAЁЂBСНжжЩЬЦЗЙВ200МўЃЌЦфжаЙКНјAжжЩЬЦЗxМўЃЌЪЕМЪНјЛѕЪБЃЌЩњВњГЇМвЖдAжжЩЬЦЗЕФГіГЇМлЯТЕїaЃЈ50ЃМaЃМ70ЃЉдЊГіЪлЃЌШєЩЬГЁБЃГжЭЌжжЩЬЦЗЕФЪлМлВЛБфЃЌЩЬГЁЪлЭъет200МўЩЬЦЗЕФзмРћШѓЮЊyдЊЃЎ
ЂйЧѓyЙигкxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЂкШєЯоЖЈAжжЩЬЦЗзюЖрЙКНј120МўзюЩйЙКНј100МўЃЌЧыФуИљОнвдЩЯаХЯЂЃЌЩшМЦГіЪЙИУЩЬГЁЛёЕУзюДѓРћШѓЕФНјЛѕЗНАИЃЎ





