题目内容
【题目】如图,正方形![]() 的边长是4,
的边长是4,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,若点
,若点![]() 、
、![]() 分别是
分别是![]() 和
和![]() 上的动点,则
上的动点,则![]() 的最小值是__________.
的最小值是__________.

【答案】![]()
【解析】
过![]() 作
作![]() 的垂线交
的垂线交![]() 于F,交AC于D′,再过D′作D′P′⊥AD,由角平分线的性质可得出D′是D关于AE的对称点,进而可知D′P′即为DQ+PQ的最小值.
于F,交AC于D′,再过D′作D′P′⊥AD,由角平分线的性质可得出D′是D关于AE的对称点,进而可知D′P′即为DQ+PQ的最小值.
解:过![]() 作
作![]() 的垂线交
的垂线交![]() 于F,交AC于D′,再过D′作D′P′⊥AD,如下图,
于F,交AC于D′,再过D′作D′P′⊥AD,如下图,
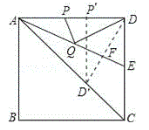
∵DD′⊥AE,
∴∠AFD=∠AFD′,
∵AF=AF,∠DAE=∠CAE,
∴△DAF≌△D′AF,
∴D′是D关于AE的对称点,AD′=AD=4,
∴D′P′即为DQ+PQ的最小值,
∵四边形ABCD是正方形,
∴∠DAD′=45°,
∴AP′=P′D′,
在Rt△AP′D′中,
P′D′2+AP′2=AD′2,AD′2=16,
∵AP′=P′D',
2P′D′2=AD′2,即2P′D′2=16,
∴P′D′=![]() ,
,
即![]() 的最小值是
的最小值是![]() .
.
故答案为:![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目