题目内容
【题目】如图,在矩形ABCD中,AB=2,AD=5,过点A、B作⊙O,交AD,BC于点E,F,连接BE,CE,过点F作FG⊥CE,垂足为G.
(1)当点F是BC的中点时,求证:直线FG与⊙O相切;
(2)若FG∥BE时,求AE的长.
【答案】
(1)证明:连接OF,
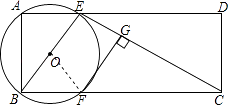
∵点F是BC的中点,
∴BF=CF,
在矩形ABCD中,∵∠A=90°,
∴BE是⊙O的直径,
∴BO=OE,
∴OF∥CE,
∵FG⊥CE,
∴OF⊥FG,
∴直线FG与⊙O相切
(2)解:∵FG∥BE,FG⊥CE,
∴BE⊥CE,
∴∠AEB+∠DEC=90°,
∵∠ABE+∠AEB=90°,
∴∠ABE=∠DEC,
∵∠A=∠D=90°,
∴△ABE∽△CDE,
∴ ![]() ,
,
∵AB=2,AD=5,
∴CD=AB=2,
∴ ![]() ,
,
∴AE=1,或AE=4.
【解析】(1)连接OF,由点F是BC的中点,得BF=CF,在矩形ABCD中,∵∠A=90°,得BE是⊙O的直径,求得BO=OE,根据三角形得中位线得OF∥CE,证得OF⊥FG即可;(2)根据平行线的性质得到BE⊥CE,由余角的性质得到∠ABE=∠DEC证得△ABE∽△CDE,根据相似三角形得性质就可求出答案。
【考点精析】关于本题考查的平行线的性质和三角形中位线定理,需要了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能得出正确答案.

 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案【题目】郴州市一座美丽的旅游城市,吸引了很多的外地游客,某旅行社对5月份本社接待的外地游客来郴州旅游的首选景点作了一次抽样调查.调查结果如下图表:(如图)
景点 | 频数 | 频率 |
东江湖 |
|
|
莽山 |
|
|
飞天山 |
| |
苏仙岭 |
|
|
万华岩 |
|
|

![]() 此次共调查了多少人?
此次共调查了多少人?
![]() 请将以上图表补充完整.
请将以上图表补充完整.
![]() 该旅行社预计6月份接待外地来郴的游客
该旅行社预计6月份接待外地来郴的游客![]() 人,请你估计首选去东江湖的人数约有多少人.
人,请你估计首选去东江湖的人数约有多少人.











