题目内容
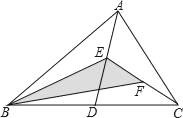
【题目】已知：在
中，
，
，过点
、
分别作
的垂线与过点
的直线交于
、
两点.
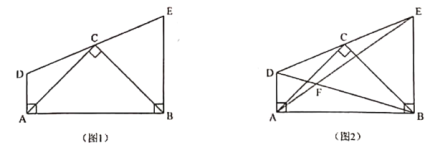
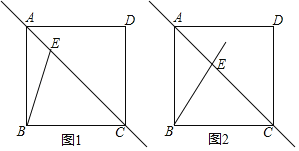
（1）如图1，求证：
；
（2）如图2，连接
、
相交于点
，在不添加任何辅助线的情况下，请写出图2中的四对三角形，使写出的每对三角形面积相等.
【答案】（1）详见解析；（2）详见解析.
【解析】
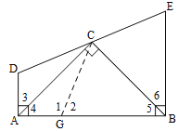
（1）在AB上截取AG=AD，通过证明△ADC≌△AGC，可得∠D=∠1，由补角的性质可得∠2=∠E，通过证明△BCG≌△BCE，可得BG=BE，即可得结论；
（2）由等底等高的两个三角形面积相等和三角形中线性质可求解．
（1）证明：在
上取一点
，使得
，
∵
中，
，
，
，
，
∴
，
在
和
中，，
，
，
∴
（SAS），
∴
，
∵，，
∴
，
∴
，
∴
，
∴
，
又∵
，
∴
，
在
和
中，
，，
，
∴
（AAS），
∴
，
∴
；
（2））∵AD∥BE，
∴S△EAD=S△BAD，S△ABE=S△DEB，
∴S△EDF=S△FAB，
由（1）可知，DC=CE=CG，
∴S△BCD=S△BCE，
∴△EAD和△BAD，△AEB和△DEB，△FDE和△FAB，△BCE和△BCD，每对三角形面积相等．
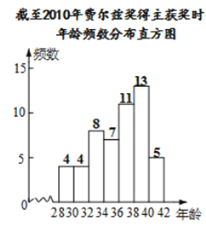
阅读快车系列答案
【题目】下面数据是截至2010年费尔兹奖得主获奖时的年龄：
29 39 35 33 39 28 33 35 31 31 37 32 38
36 31 39 32 38 37 34 29 34 38 32 35 36
33 29 32 35 36 37 39 38 40 38 37 39 38
34 33 40 36 36 37 40 31 38 38 40 40 37
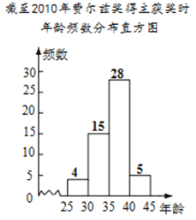
小果、小冻、小甜将数据整理，分别按组距是2，5，10进行分组，列出频数分布表，画出频数分布直方图，如下：
年龄 | 频数 |
| 4 |
| 4 |
| 8 |
| 7 |
| 11 |
| 13 |
| 5 |
年龄 | 频数 |
| 4 |
| 15 |
| 28 |
| 5 |
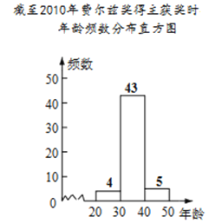
年龄 | 频数 |
| 4 |
| 43 |
| 5 |
根据以上材料回答问题：
小果、小冻、小甜三人中，比较哪一位同学分组能更好的说明费尔兹奖得主获奖时的年龄分布，并简要说明其他两位同学分组的不足之处．
费尔兹奖是国际上享有崇高声誉的一个数学奖项，每4年评选一次，主要授予年轻的数学家，美籍华人丘成桐（1949年出生）1982年获费尔兹奖．
