题目内容
【题目】在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(﹣ 2,﹣ 2),(![]() ,
, ![]() ),…,都是梦之点,显然梦之点有无数个.
),…,都是梦之点,显然梦之点有无数个.
(1)若点 P(2,b)是反比例函数![]() (n 为常数,n ≠ 0) 的图象上的梦之点,求这个反比例函数解析式;
(n 为常数,n ≠ 0) 的图象上的梦之点,求这个反比例函数解析式;
(2)⊙ O 的半径是![]() ,
,

①求出⊙ O 上的所有梦之点的坐标;
②已知点 M(m,3),点 Q 是(1)中反比例函数![]() 图象上异于点 P 的梦之点,过点Q 的直线 l 与 y 轴交于点 A,tan∠OAQ= 1.若在⊙ O 上存在一点 N,使得直线 MN ∥ l或 MN ⊥ l,求出 m 的取值范围.
图象上异于点 P 的梦之点,过点Q 的直线 l 与 y 轴交于点 A,tan∠OAQ= 1.若在⊙ O 上存在一点 N,使得直线 MN ∥ l或 MN ⊥ l,求出 m 的取值范围.
【答案】(1)反比例函数解析式为![]() ;
;
(2)①⊙ O 上的所有梦之点的坐标为(1,1)或(-1,-1);②m 的取值范围是-5≤m≤-1或1≤m≤5.
【解析】试题分析:(1)由梦之点坐标特点可得b=2,再将P坐标代入![]() 中,即可求得n的值;(2)①设⊙O上梦之点坐标是(a,a),由圆的半径是
中,即可求得n的值;(2)①设⊙O上梦之点坐标是(a,a),由圆的半径是![]() 得:
得: ![]()
则a=1或a=-1,所以⊙O上所有梦之点坐标是(1,1)或(-1,-1);② 由(1)可得,异于点P的梦之点是(-2,-2),设直线MN为y=-x+b,求得m的取值范围;当直线MN为y=x+b时,求得m的取值范围;
试题解析:
解:(1) ∵P(2,b)是梦之点
∴b=2
∴P(2,2)
将P(2,2) 代入![]() 中得n=4
中得n=4
∴反比例函数解析式是![]()
(2) ①∵⊙O的半径是![]()
设⊙O上梦之点坐标是(a,a)
∴![]()
∴![]()
a=1或a=-1
∴⊙O上所有梦之点坐标是(1,1)或(-1,-1)
②由(1)知,异于点P的梦之点是(-2,-2)
∵tan∠OAQ=1
∴∠OAQ==45°
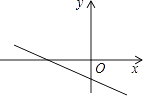
由已知MN∥l或MN⊥l,如图所示:
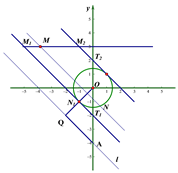
∴直线MN为y=-x+b或y=x+b
当MN为y=-x+b时,m=b-3
由图可知,当直线MN平移至与⊙O相切时,
且切点在第四 象限时,b取得最小值,
此时MN 记为![]() ,
,
其中 ![]() 为切点,
为切点, ![]() 为直线与y轴的交点。
为直线与y轴的交点。
∵△O![]()
![]() 为等要直角三角形,
为等要直角三角形,
∴O![]() =
=![]() ∴O
∴O![]() =2
=2
∴b的最小值是-2,
∴m的最小值是-5
当直线MN平移至与⊙O相切时,且切点在第二象限时,
b取得最大值,此时MN 记为![]() ,
,
其中 ![]() 为切点,
为切点, ![]() 为直线
为直线![]() 与y轴的交点。
与y轴的交点。
同理可得,b的最大值为2,m的最大值为-1.
∴m的取值范围为-5≤m≤-1
当直线MN为y=x+b时,
同理可得,m的取值范围为1≤m≤5,
综上所述,m的取值范围为-5≤m≤-1或1≤m≤5.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案