题目内容
【题目】在平面直角坐标系xOy中,抛物线y=ax2+2ax﹣3a(a>0)与x轴交于A,B两点(点A在点B的左侧).
(1)求抛物线的对称轴及线段AB的长;
(2)抛物线的顶点为P,若∠APB=120°,求顶点P的坐标及a的值;
(3)若在抛物线上存在一点N,使得∠ANB=90°,结合图象,求a的取值范围.
【答案】(1) x=﹣1 , AB=4 ;(2) 点P的坐标为(﹣1,﹣ ![]() ).a=
).a= ![]() ; (3) a≥
; (3) a≥ ![]() .
.
【解析】(1)、根据题意求出点A和点B的坐标,从而得出对称轴;(2)、设抛物线的对称轴与x轴交于点H,根据题意得出AH和PH的长度,从而得出点P的坐标,将其代入函数解析式得出a的值;(3)、以AB为直径作⊙H, 当∠ANB=90°, 点N在⊙H上,将x=-1代入y=-4a得出HP的长度,根据题意得出a的取值范围.
(1)、解:令y=0得:ax2+2ax﹣3a=0,即a(x+3)(x﹣1)=0,解得:x=﹣3或x=1,
∴A(﹣3,0)、B(1,0), ∴抛物线的对称轴为直线x=﹣1,AB=4;
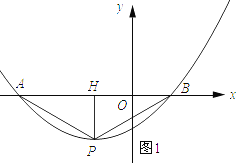
(2)、解:如图1所示:设抛物线的对称轴与x轴交于点H,
∵∠APB=120°,AB=4,PH在对称轴上, ∴AH=2,∠APB=60°, ∴PH= ![]() ,
,
∴点P的坐标为(﹣1,﹣ ![]() ),将点P的坐标代入得:﹣
),将点P的坐标代入得:﹣ ![]() =﹣4a,解得a=
=﹣4a,解得a= ![]() ;
;
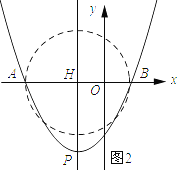
(3)、解:如图2所示:以AB为直径作⊙H, ∵当∠ANB=90°, ∴点N在⊙H上,
∵点N在抛物线上, ∴点N为抛物线与⊙H的交点, ∴点P在圆上或点P在圆外,
∴HP≥2, ∵将x=﹣1代入得:y=﹣4a, ∴HP=4a, ∴4a≥2,解得a≥ ![]() ,
,
∴a的取值范围是a≥ ![]() .
.

 应用题作业本系列答案
应用题作业本系列答案【题目】下表中有两种移动电话计费方式.设一个月内用移动电话主叫为![]()
![]() (
(![]() 是正整数).
是正整数).
月使用费/元 | 主叫限定时间/min | 主 叫 超 时费/(元/min) | 被叫 | |
方式一 | 58 | 150 | 0.25 | 免费 |
方式二 | 88 | 350 | 0.19 | 免费 |
(1)根据上表,补全下列表.
主叫时间 | 方式一计费/元 | 方式二计费/元 |
| 58 | 88 |
| 58 | 88 |
|
| 88 |
|
| 88 |
|
|
(2)观察(1)中表格,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
(3)小明本月通话时间![]() 分钟.如果采用方式二付费比方式一付费少20.6元;如果通话时间减少70分钟,采用方式二付费比方式一付费少5元.你能确定小明本月通话时长吗?请你通过计算说明.
分钟.如果采用方式二付费比方式一付费少20.6元;如果通话时间减少70分钟,采用方式二付费比方式一付费少5元.你能确定小明本月通话时长吗?请你通过计算说明.