Question

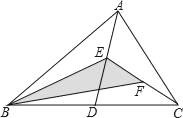
【题目】如图，在△ABC中，已知点D、E、F分别为边BC、AD、CE的中点，若△ABC的面积为16，则图中阴影部分的面积为_____．

Answer 1

【答案】4.

【解析】

因为点F是CE的中点，所以△BEF的底是△BEC的底的一半，△BEF高等于△BEC的高；同理，D、E、分别是BC、AD的中点，可得△EBC的面积是△ABC面积的一半；利用三角形的等积变换可解答．

解：解：如图，

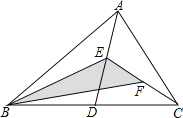
点F是CE的中点，
∴△BEF的底是EF，△BEC的底是EC，即EF=EC，而高相等，
∴S△BEF= S△BEC，
∵E是AD的中点，
∴S△BDE= S△ABD，S△CDE= S△ACD，
∴S△EBC= S△ABC，
∴S△BEF= S△ABC，且S△ABC=16，
∴S△BEF=4，
即阴影部分的面积为4cm2．

故答案为4．