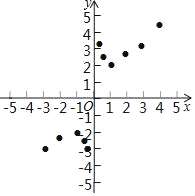��Ŀ����
����Ŀ�����ݡ�̫ԭ�е綯���г������������Ĺ涨��2019��5��1����δ���Ƶĵ綯���г�����ֹ��·��ʻ�����綯���г����ƵǼDZ���������ұ���ij�̵깺���˼ף������ַ��Ϲ��ұ����¿�綯���г������м��ֳ��ܽ���Ϊ22500Ԫ�����ֳ��ܽ���Ϊ45000Ԫ����֪���ֳ�ÿ���Ľ����Ǽ��ֳ����۵�1.5�����ҹ����ļ��ֳ������ֳ���5����
(1)���ֵ綯���г�ÿ���Ľ����Ƕ���Ԫ��
(2)�����綯���г����к�ܿ�����һ�գ����̵�ƻ���ԭ�����ٴι��������ֵ綯���г���50�������¹����ĵ綯���г����ձ����е��ۼ����ۣ����¹������ֳ�m��(20��m��30)�����ֳ�ȫ���۳���������ΪyԪ(���������ɱ�)��
����y��m֮��ĺ�����ϵʽ��
���̵��������Ž�������������ʹ�����������綯���г���õ����������������Ƕ��٣�
�ͺ� | �� | �� |
�ۼ�(Ԫ/��) | 2000 | 2800 |
���𰸡�(1)�綯���Ľ���Ϊÿ��1500Ԫ��(2)��y����50m+27500���ڵ�x��20ʱ����������������Ϊ26500Ԫ��
��������
��1�����ݼס������ֵ綯���Ľ��ۡ�����֮��Ĺ�ϵ���з�ʽ���̽��н�ɣ�
��2����������yԪ��綯��������m֮��ĺ�����ϵʽ�������ݺ����������Ժ��Ա�����ȡֵ��Χ��ȷ����ʱ�������
�⣺(1)����ֵ綯���г�ÿ���Ľ�����xԪ�������ֵ綯���Ľ���Ϊ1.5xԪ��������ã�
![]() ��
��
��ã�x��1500��
�����飬x��1500��ԭ���̵Ľ⣬
�𣺼綯���Ľ���Ϊÿ��1500Ԫ��
(2)�����¹������ֳ�m�������ҵ綯��Ϊ(50��m)����
y��(2000��1500)m+(2800��1500��1.5)(50��m)����50m+27500
�ڡ�y����50m+27500��y��x���������С��20��m��30��
����x��20ʱ��y�������50��20+27500��26500Ԫ��
��y��x�ĺ�����ϵʽΪy����50x+27500����x��20ʱ����������������Ϊ26500Ԫ��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��С������ѧϰ�����ľ��飬�Ժ���y=x+![]() ��ͼ�������ʽ�����̽����
��ͼ�������ʽ�����̽����
������С����̽�����̣��벹��������
��1������y=x+![]() ���Ա���x��ȡֵ��Χ��_____��
���Ա���x��ȡֵ��Χ��_____��
��2���±��г���y��x�ļ����Ӧֵ����д��m��n��ֵ��m=_____��n=_____��
x | �� | ��3 | ��2 | ��1 | �� | �� |
|
| 1 | 2 | 3 | 4 | �� |
y | �� | �� | �� | ��2 | �� | �� | m |
| 2 |
| n |
| �� |
��3����ͼ����ƽ��ֱ������ϵxOy�У���������ϱ��и��Զ�ӦֵΪ����ĵ㣬��������ĵ㣬�����ú�����ͼ����
��4����Ϻ�����ͼ������ɣ�
�ٵ�y=��![]() ʱ��x=_____��
ʱ��x=_____��
��д���ú�����һ������_____��
��������x+![]() =t����������ȵ�ʵ��������t��ȡֵ��Χ��_____��
=t����������ȵ�ʵ��������t��ȡֵ��Χ��_____��