Question

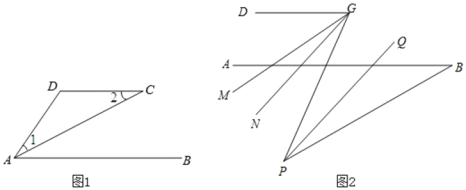
【题目】（1）如图1，AC平分DAB，12，试说明AB与CD的位置关系，并予以证明：

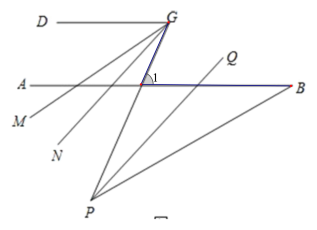
（2）如图2，在（1）的结论下，AB的下方点P满足ABP30，G是CD上任一点，PQ平分BPG，PQ∥GN，GM平分DGP，下列结论：

①DGPMGN的值不变；

②MGN的度数不变．

可以证明，只有一个是正确的，请你做出正确的选择并求值．

Answer 1

【答案】（1）见详解；（2）②正确，MGN的度数为15°，理由见详解．

【解析】

（1）由AC平分DAB，12，可得∠2=∠BAC,进而即可得到结论；

（2）由角平分线的定义和三角形外角的性质，可得∠MGP=（∠BPG+∠B），由PQ∥GN，得∠NGP=∠GPQ=∠BPG，进而由∠MGN=∠MGP-∠NGP，即可得到结论．

（1）AB∥CD，理由如下：

∵AC平分DAB，

∴∠1=∠BAC，

∵12，

∴∠2=∠BAC,

∴AB∥CD；

（2）②MGN的度数不变是正确的，理由如下：

∵PQ平分BPG，GM平分DGP，

∴∠GPQ=∠BPG，∠MGP=∠DGP，

∵AB∥CD，

∴∠1=∠DGP，

∵∠1=∠BPG+∠B，

∴∠MGP=∠1=（∠BPG+∠B），

∵PQ∥GN，

∴∠NGP=∠GPQ=∠BPG，

∴∠MGN=∠MGP-∠NGP=（∠BPG+∠B）-∠BPG=∠B=×30°=15°，

∴MGN的度数不变，度数为15°．