题目内容
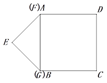
【题目】如图，在六边形ABCDEF中，AF∥CD，A140，C165．
（1）求B的度数；
（2）当D °时，AB∥DE？为什么？
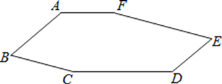
【答案】（1）°；（2）140°
【解析】
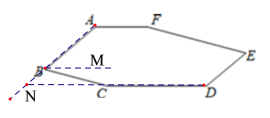
（1）过点B作BM∥AF，则BM∥AF∥CD，A140，C165，进而即可求解；
（2）延长AB，DC交于点N，由∠ABC=55°，CD165,得∠C=40°，结合AB∥DE，即可得到答案．
（1）过点B作BM∥AF，
∵AF∥CD，
∴BM∥AF∥CD，
∴∠A+∠ABM=180°，∠C+∠CBM=180°，
∵A140，C165，
∴B=∠ABM+∠CBM=360°-∠A-∠C=360°-140-165°．
（2）延长AB，DC交于点N，
∵∠ABC=55°，
∴∠NBC=125°，
∵CD165,
∴∠C165125°=40°
若AB∥DE，则∠D=180°-40°=140°．
故答案是：140°
练习册系列答案
特高级教师点拨系列答案
相关题目
