Question

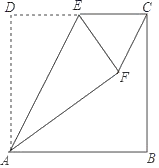
【题目】如图，正方形ABCD中，AB＝6，E是CD的中点，将△ADE沿AE翻折至△AFE，连接CF，则CF的长度是_____．

Answer 1

【答案】

【解析】

连接DF交AE于G，依据轴对称的性质以及三角形内角和定理，即可得到∠AGD＝∠DFC＝90°，再根据面积法即可得出DG＝，最后判定△ADG≌△DCF，即可得到CF＝DG＝．

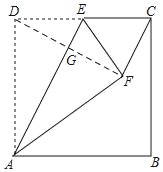
解：如图，连接DF交AE于G，

由折叠可得，DE＝EF，

又∵E是CD的中点，

∴DE＝CE＝EF，

∴∠EDF＝∠EFD，∠ECF＝∠EFC，

又∵∠EDF+∠EFD+∠EFC+∠ECF＝180°，

∴∠EFD+∠EFC＝90°，即∠DFC＝90°，

由折叠可得AE⊥DF，

∴∠AGD＝∠DFC＝90°，

又∵ED＝3，AD＝6，

∴Rt△ADE中，

又∵

∴DG＝

∵∠DAG+∠ADG＝∠CDF+∠ADG＝90°，

∴∠DAG＝∠CDF，

又∵AD＝CD，∠AGD＝∠DFC＝90°，

∴△ADG≌△DCF（AAS），

∴CF＝DG＝，

故答案为：．