题目内容
【题目】如图,直线y=x﹣4与x轴、y轴分别交于M、N两点,以坐标原点O为圆心的⊙O半径为2,将⊙O沿x轴向右平移,当⊙O恰好与直线MN相切时,平移的最小距离为 . 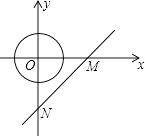
【答案】4﹣2 ![]()
【解析】解:如图,设⊙O′与直线MN相切于点H.
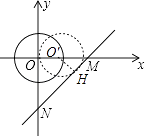
由题意OM=ON=4,∠OMN=45°
在Rt△O′HM中,∵O′H=2,
∴O′M=2 ![]() ,
,
∴OO′=4﹣2 ![]() ,
,
∴当⊙O恰好与直线MN相切时,平移的最小距离为4﹣2 ![]() .
.
【考点精析】本题主要考查了切线的性质定理和解直角三角形的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】在学习三角形中位线的性质时,小亮对课本给出的解决办法进行了认真思考:
课本研究三角形中位线性质的方法 |
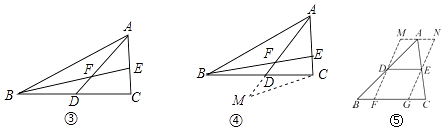

请你利用小亮的发现解决下列问题:
(1)如图③,AD是△ABC的中线,BE交AC于点E,交AD于点F,且AE=EF,求证:AC=BF.
请你帮助小亮写出辅助线作法并完成论证过程:
(2)解决问题:如图⑤,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线.过点D,E作DF∥EG,分别交BC于点F,G,过点A作MN∥BC,分别与FD,GE的延长线交于点M,N,则四边形MFGN周长的最小值是 .