题目内容
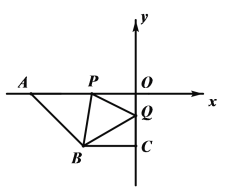
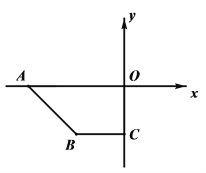
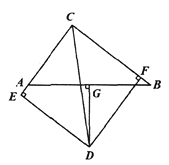
【题目】如图,△ABC中,AC=6,BC=8,AB=10,∠BCA的平分线与AB的垂直平分线DG交于点D,DE⊥CA的延长线于点E,DF⊥CB于点F.
(1)判断△ABC的形状,并说明理由;
(2)求证:AE=BF;
(3)求DG的长.
【答案】(1)直角三角形;(2)过程见解析;(3)5.
【解析】
(1)根据勾股定理的逆定理即可判断△ABC是直角三角形;
(2)根据中垂线、角平分线的性质来证明Rt△AED≌Rt△BFD,然后根据全等三角形的对应边相等推知AE=BF;
(3)首先根据(1)和(2)得出的结论,证明△ADB是直角三角形,再利用三线合一的性质和直角三角形斜边上的中线等于斜边的一半,进而得出DG.
解:(1)∵AC=6,BC=8,AB=10,
∴AC2+BC2=AB2,
∴△ABC是直角三角形;
(2)证明:连接AD、BD,
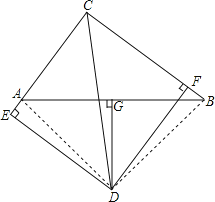
∵CD是∠BCA的平分线,DE⊥AC,DF⊥BC,
∴DE=DF,
∵DG是AB边的垂直平分线,
∴DA=DB,
在Rt△AED和Rt△BFD中,
![]()
∴Rt△AED≌Rt△BFD(HL),
∴AE=BF;
(3)由(1)得∠ACB=90°,
∵∠E=∠DFC=90°
∴∠EDF=90°,
由(2)知∠EDA=∠FDB,
∴∠ADB=90°,
∵DG⊥AB,DA=DB,
∴DG=![]() AB=5.
AB=5.
故答案为:(1)直角三角形;(2)过程见解析;(3)5.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值 |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若每袋标准质量为450克,则抽样检测的总质量是多少?