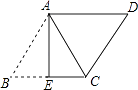
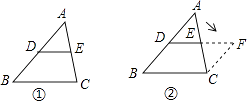题目内容
【题目】在学习三角形中位线的性质时,小亮对课本给出的解决办法进行了认真思考:
课本研究三角形中位线性质的方法 |
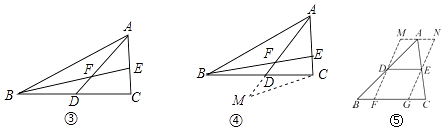

请你利用小亮的发现解决下列问题:
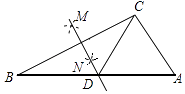
(1)如图③,AD是△ABC的中线,BE交AC于点E,交AD于点F,且AE=EF,求证:AC=BF.
请你帮助小亮写出辅助线作法并完成论证过程:
(2)解决问题:如图⑤,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线.过点D,E作DF∥EG,分别交BC于点F,G,过点A作MN∥BC,分别与FD,GE的延长线交于点M,N,则四边形MFGN周长的最小值是 .
【答案】
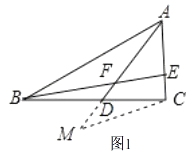
(1)证明:如图1,延长AD至点M,使MD=FD,连接MC,
在△BDF和△CDM中,BD=CD,∠BDF=∠CDM,DF=DM.
∴△BDF≌△CDM(SAS).
∴MC=BF,∠M=∠BFM.
∵EA=EF,
∴∠EAF=∠EFA.
∵∠AFE=∠BFM,
∴∠M=∠MAC.
∴AC=MC.
∴BF=AC.
(2)8+10 ![]()
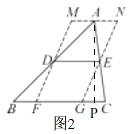
【解析】(2)如图2,
在△ABC中,∠B=45°,AB=10,BC=8,
∵DE是△ABC的中位线.
∴DE= ![]() BC=4,DE∥BC
BC=4,DE∥BC
∵DF∥EG,MN∥BC,
∴四边形DEGF,DENM,FGNM是平行四边形,
∴MN=FG=DE=4,
∴要四边形MFGN周长的最小只有MF=NG最小,
即:MF⊥BC,
∴平行四边形FGNM是矩形,
过点A作AP⊥BC于P,
∴AP=MF=NG,
在Rt△ABP中,∠B=45°,AB=10,
∴AP=5 ![]() ,
,
∴MF=NG=5 ![]() ,
,
即四边形MFGN周长的最小值是8+10 ![]() .
.
所以答案是:8+10 ![]() .
.
【考点精析】利用三角形中位线定理对题目进行判断即可得到答案,需要熟知连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.