��Ŀ����
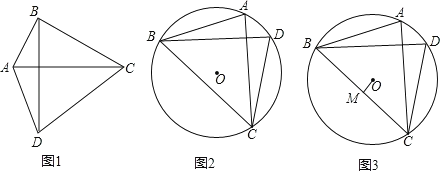
����Ŀ����ͼ��ʾ,����ABC��,AB=AC=2,BC=2![]() ,��A=90��.ȡһ�麬45���ǵ�ֱ�����dz�,��ֱ�Ƕ������б��BC���е�O��,һ��ֱ�DZ߹���A(��ͼ1).���dz��Ƶ�O˳ʱ�뷽����ת,ʹ90���ǵ�������Rt��ABC������AB,AC�ֱ��ཻ�ڵ�E,F(��ͼ2).��BE=x,CF=y.
,��A=90��.ȡһ�麬45���ǵ�ֱ�����dz�,��ֱ�Ƕ������б��BC���е�O��,һ��ֱ�DZ߹���A(��ͼ1).���dz��Ƶ�O˳ʱ�뷽����ת,ʹ90���ǵ�������Rt��ABC������AB,AC�ֱ��ཻ�ڵ�E,F(��ͼ2).��BE=x,CF=y.
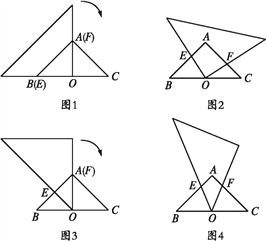
(1)̽��:��ͼ2��,�߶�AE��CF�������Ĵ�С��ϵ?֤����Ľ���.
(2)����������ת������y��x�ĺ�������ʽ,��д��x��ȡֵ��Χ.
(3)����ֱ�����dz�45���ǵĶ������б��BC�ߵ��е�O��,һ��ֱ�DZ߹���A(��ͼ3).���dz���O��˳ʱ�뷽����ת,ʹ45���ǵ�������Rt��ABC������AB,AC�ֱ��ཻ�ڵ�E,F(��ͼ4).�����dz��Ƶ�O��ת�Ĺ�����,��OEF�Ƿ��ܳ�Ϊ����������?����,ֱ��д����OEFΪ����������ʱx��ֵ;������,��˵������.
���𰸡�(1)AE=CF��(2) y=2-x��0��x��2����(3)��OEFΪ����������ʱx��ֵΪ1��![]() ��2.
��2.
�������������������1�����ȵó�����EAO=��C=45�㣬AO=OC����EOA=��FOC�������ó���EOA�ա�FOC�����ɵó��𰸣�
��2������AE=CF���ó�BE+CF=BE+AE=AB=2����x+y=2�����ɵó��𰸣�
��3������OE=EFʱ����EΪAB�е㣬��F���A�غϣ���OE=OFʱ��BE=BO=CO=CF=![]() ����EF=OFʱ����E���A�غϣ���FΪAC�е㣬�����ó��𰸣�
����EF=OFʱ����E���A�غϣ���FΪAC�е㣬�����ó��𰸣�
�����������1��AE=CF��
���ɣ�����AO����ͼ2��
��AB=AC����OΪBC���е㣬��BAC=90�㣬
���AOC=90�㣬��EAO=��C=45�㣬AO=OC��
�ߡ�EOF=90�㣬��EOA+��AOF=90�㣬��COF+��AOF=90�㣬
���EOA=��FOC��
�ڡ�EOA�͡�FOC�У�
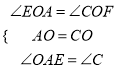 ,
,
���EOA�ա�FOC��ASA����
��AE=CF��

��2����AE=CF����BE+CF=BE+AE=AB=2����x+y=2��
��y��x�ĺ�����ϵʽ��y=2-x��
x��ȡֵ��Χ�ǣ�0��x��2��
��3����OEF�ܹ��ɵ��������Σ�
��OE=EFʱ����ͼ3����EΪAB�е㣬��F���A�غϣ�BE=AE=1����x=1��
��OE=OFʱ����ͼ4��BE=BO=CO=CF=![]() ����x=
����x=![]() ��
��
��EF=OFʱ����ͼ5����E���A�غϣ���FΪAC�е㣬��x=2��
������������OEFΪ����������ʱx��ֵΪ1��![]() ��2��
��2��


����Ŀ����ѧ��С��������ҵ�������ڼ乺��100ֻ�����ͺŵ��ľ߽������ۣ�����ۺ��ۼ�֮��Ĺ�ϵ���±���
�ͺ� | ���ۣ�Ԫ/ֻ�� | �ۼۣ�Ԫ/ֻ�� |
A�� | 10 | 12 |
B�� | 15 | 23 |
Ҫʹ�����ľ����������������۸��40%��������Ҫ��������ֻA���ľߣ�