ЬтФПФкШн
ЁОЬтФПЁПШєвЛИіЫФБпаЮЕФСНЬѕЖдНЧЯпЛЅЯрДЙжБЧвЯрЕШЃЌдђГЦетИіЫФБпаЮЮЊЁАЦцУюЫФБпаЮЁБЃЎШчЭМ1ЃЌЫФБпаЮABCDжаЃЌШєAC=BDЃЌACЁЭBDЃЌдђГЦЫФБпаЮABCDЮЊЦцУюЫФБпаЮЃЎИљОнЁАЦцУюЫФБпаЮЁБЖдНЧЯпЛЅЯрДЙжБЕФЬиеїПЩЕУЁАЦцУюЫФБпаЮЁБЕФвЛИіживЊаджЪЃКЁАЦцУюЫФБпаЮЁБЕФУцЛ§ЕШгкСНЬѕЖдНЧЯпГЫЛ§ЕФвЛАыЃЎИљОнвдЩЯаХЯЂЛиД№ЃК
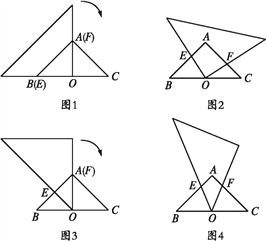
ЃЈ1ЃЉОиаЮ ЁАЦцУюЫФБпаЮЁБЃЈЬюЁАЪЧЁБЛђЁАВЛЪЧЁБЃЉЃЛ
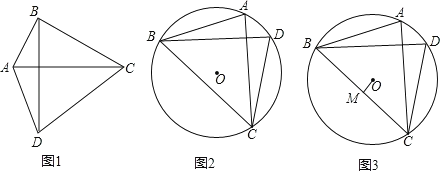
ЃЈ2ЃЉШчЭМ2ЃЌвбжЊЁбOЕФФкНгЫФБпаЮABCDЪЧЁАЦцУюЫФБпаЮЁБЃЌШєЁбOЕФАыОЖЮЊ6ЃЌЁЯBCD=60ЁуЃЎЧѓЁАЦцУюЫФБпаЮЁБABCDЕФУцЛ§ЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌвбжЊЁбOЕФФкНгЫФБпаЮABCDЪЧЁАЦцУюЫФБпаЮЁБзїOMЁЭBCгкMЃЎЧыВТВтOMгыADЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЎ
ЁОД№АИЁПЃЈ1ЃЉЪЧЃЛЃЈ2ЃЉ54.ЃЈ3ЃЉAD=2OMЃЌжЄУїМћНтЮіЁЃ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнОиаЮЕФаджЪКЭЁАЦцУюЫФБпаЮЁБЕФЖЈвхНјааХаЖЯЃЛ
ЃЈ2ЃЉСЌНсOBЁЂODЃЌзїOHЁЭBDгкHЃЌШчЭМ2ЃЌИљОнДЙОЖЖЈРэЕУЕНBH=DHЃЌИљОндВжмНЧЖЈРэЕУЕНЁЯBOD=2ЁЯBCD=120ЁуЃЌдђРћгУЕШбќШ§НЧаЮЕФаджЪЕУЁЯOBD=30ЁуЃЌдкRtЁїOBHжаПЩМЦЫуГіBH=![]() OH=3
OH=3![]() ЃЌBD=2BH=6
ЃЌBD=2BH=6![]() ЃЌдђAC=BD=6
ЃЌдђAC=BD=6![]() ЃЌШЛКѓИљОнЦцУюЫФБпаЮЁБЕФУцЛ§ЕШгкСНЬѕЖдНЧЯпГЫЛ§ЕФвЛАыЧѓНтЃЛ
ЃЌШЛКѓИљОнЦцУюЫФБпаЮЁБЕФУцЛ§ЕШгкСНЬѕЖдНЧЯпГЫЛ§ЕФвЛАыЧѓНтЃЛ
ЃЈ3ЃЉСЌНсOBЁЂOCЁЂOAЁЂODЃЌзїOEЁЭADгкEЃЌШчЭМ3ЃЌИљОнДЙОЖЖЈРэЕУЕНAE=DEЃЌдйРћгУдВжмНЧЖЈРэЕУЕНЁЯBOM=ЁЯBACЃЌЁЯAOE=ЁЯABDЃЌдйРћгУЕШНЧЕФгрНЧЯрЕШЕУЕНЁЯOBM=ЁЯAOEЃЌдђПЩжЄУїЁїBOMЁеЁїOAEЕУЕНOM=AEЃЌгкЪЧгаOM=![]() ADЃЎ
ADЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉОиаЮЕФЖдНЧЯпЯрЕШЕЋВЛДЙжБЃЌ
ЫљвдОиаЮВЛЪЧЁАЦцУюЫФБпаЮЁБЃЛ
ЙЪД№АИЮЊВЛЪЧЃЛ
ЃЈ2ЃЉСЌНсOBЁЂODЃЌзїOHЁЭBDгкHЃЌШчЭМ2ЃЌдђBH=DHЃЌ
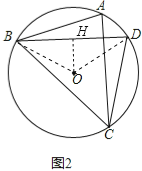
ЁпЁЯBOD=2ЁЯBCD=2ЁС60Ёу=120ЁуЃЌ
ЁрЁЯOBD=30ЁуЃЌ
дкRtЁїOBHжаЃЌЁпЁЯOBH=30ЁуЃЌ
ЁрOH=![]() OB=3ЃЌ
OB=3ЃЌ
ЁрBH=![]() OH=3
OH=3![]() ЃЌ
ЃЌ
ЁпBD=2BH=6![]() ЃЌ
ЃЌ
ЁрAC=BD=6![]() ЃЌ
ЃЌ
ЁрЁАЦцУюЫФБпаЮЁБABCDЕФУцЛ§=![]() ЁС6
ЁС6![]() ЁС6
ЁС6![]() =54ЃЛ
=54ЃЛ
ЃЈ3ЃЉOM=![]() ADЃЎРэгЩШчЯТЃК
ADЃЎРэгЩШчЯТЃК
СЌНсOBЁЂOCЁЂOAЁЂODЃЌзїOEЁЭADгкEЃЌШчЭМ3ЃЌ
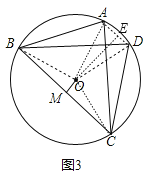
ЁпOEЁЭADЃЌ
ЁрAE=DEЃЌ
ЁпЁЯBOC=2ЁЯBACЃЌ
ЖјЁЯBOC=2ЁЯBOMЃЌ
ЁрЁЯBOM=ЁЯBACЃЌ
ЭЌРэПЩЕУЁЯAOE=ЁЯABDЃЌ
ЁпBDЁЭACЃЌ
ЁрЁЯBAC+ЁЯABD=90ЁуЃЌ
ЁрЁЯBOM+ЁЯAOE=90ЁуЃЌ
ЁпЁЯBOM+ЁЯOBM=90ЁуЃЌ
ЁрЁЯOBM=ЁЯAOEЃЌ
дкЁїBOMКЭЁїOAEжа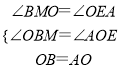
ЁрЁїBOMЁеЁїOAEЃЌ
ЁрOM=AEЃЌ
ЁрOM=![]() ADЃЎ
ADЃЎ