题目内容
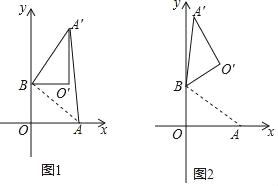
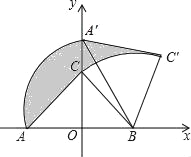
【题目】如图，Rt△ABC中，∠ACB=90°，在以AB的中点O为坐标原点，AB所在直线为x轴建立的平面直角坐标系中，将△ABC绕点B顺时针旋转，使点A旋转至y轴的正半轴上的A′处，若AO=OB=2，则阴影部分面积为（ ）
A. 
π B. π﹣1 C. 
+1 D.
【答案】D
【解析】分析：根据等腰直角三角形的性质求出AB，再根据旋转的性质可得
，然后求出
，再根据直角三角形两锐角互余求出
即旋转角为60°，再根据S阴影=S扇形ABA′+S△A′BC′-S△ABC-S扇形CBC′=S扇形ABA′-S扇形CBC′，然后利用扇形的面积公式列式计算即可得解．
详解：∵
，AC=BC，
∴△ABC是等腰直角三角形，
∴
∵△ABC绕点B顺时针旋转点A在A′处，
∴BA′=AB，
∴BA′=2OB，
∴
∴
即旋转角为
S阴影=S扇形ABA′+S△A′BC′S△ABCS扇形CBC′,
=S扇形ABA′S扇形CBC′,
故选D.
练习册系列答案
相关题目
