题目内容
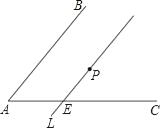
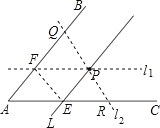
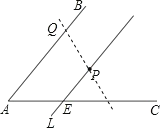
【题目】如图，∠BAC内有一点P，过点P作直线l∥AB，交AC于E点．今欲在∠BAC的两边上各找一点Q、R，使得P为QR的中点，以下是甲、乙两人的作法：
甲：①过P作直线l1∥AC，交直线AB于F点，并连接EF；
②过P作直线l2∥EF，分别交两直线AB、AC于Q、R两点，则Q、R即为所求．
乙：①在直线AC上另取一点R，使得AE=ER；
②作直线PR，交直线AB于Q点，则Q、R即为所求．
下列判断正确的是（ ）
A. 两人皆正确 B. 两人皆错误
C. 甲正确，乙错误 D. 甲错误，乙正确
【答案】A
【解析】分析：根据甲的作法可知，四边形EFQP、EFPR都是平行四边形．根据平行四边形性质可得P是QR的中点；在乙的作法中，根据平行线等分线段定理知QP=PR．
详解： (甲)由题意可知：四边形EFQP、EFPR均为平行四边形EF=QP=PR.
∴P点为QR的中点，即为所求，
故甲正确；
(乙)由题意可知：在△AQR中,∵AE=ER(即E为AR中点),且PE∥AQ，
∴P点为QR的中点,即为所求,
故乙正确.
∴甲、乙两人皆正确，故选A.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
