Question

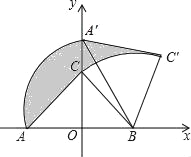
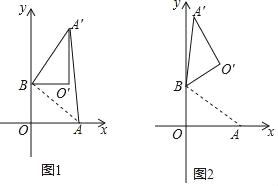
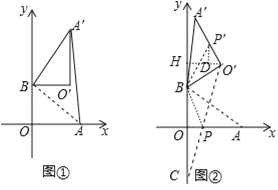
【题目】在平面直角坐标系中，O为原点，点A（8，0），点B（0，6），把△ABO绕点B逆时针旋转得△A′B′O′，点A、O旋转后的对应点为A′、O′，记旋转角为α．

（1）如图1，若α=90°，则AB=　 　，并求AA′的长；

（2）如图2，若α=120°，求点O′的坐标；

（3）在（2）的条件下，边OA上的一点P旋转后的对应点为P′，当O′P+BP′取得最小值时，直接写出点P′的坐标．

Answer 1

【答案】（1）10， ；（2）（，9）；（3）

【解析】试题分析：(1)、如图①，先利用勾股定理计算出AB=5，再根据旋转的性质得BA=BA′，∠ABA′=90°，则可判定△ABA′为等腰直角三角形，然后根据等腰直角三角形的性质求AA′的长；(2)、作O′H⊥y轴于H，如图②，利用旋转的性质得BO=BO′=3，∠OBO′=120°，则∠HBO′=60°，再在Rt△BHO′中利用含30度的直角三角形三边的关系可计算出BH和O′H的长，然后利用坐标的表示方法写出O′点的坐标；(3)、由旋转的性质得BP=BP′，则O′P+BP′=O′P+BP，作B点关于x轴的对称点C，连结O′C交x轴于P点，如图②，易得O′P+BP=O′C，利用两点之间线段最短可判断此时O′P+BP的值最小，接着利用待定系数法求出直线O′C的解析式为y=x﹣3，从而得到P（，0），则O′P′=OP=，作P′D⊥O′H于D，然后确定∠DP′O′=30°后利用含30度的直角三角形三边的关系可计算出P′D和DO′的长，从而可得到P′点的坐标．

试题解析：(1)、如图①， ∵点A（4，0），点B（0，3）， ∴OA=4，OB=3， ∴AB==5，

∵△ABO绕点B逆时针旋转90°，得△A′BO′， ∴BA=BA′，∠ABA′=90°，

∴△ABA′为等腰直角三角形， ∴AA′=BA=5；

(2)、作O′H⊥y轴于H，如图②， ∵△ABO绕点B逆时针旋转120°，得△A′BO′，

∴BO=BO′=3，∠OBO′=120°， ∴∠HBO′=60°， 在Rt△BHO′中，∵∠BO′H=90°﹣∠HBO′=30°，

∴BH=BO′=，O′H=BH=， ∴OH=OB+BH=3+， ∴O′点的坐标为（）；

（3）∵△ABO绕点B逆时针旋转120°，得△A′BO′，点P的对应点为P′， ∴BP=BP′，

∴O′P+BP′=O′P+BP， 作B点关于x轴的对称点C，连结O′C交x轴于P点，如图②，

则O′P+BP=O′P+PC=O′C，此时O′P+BP的值最小， ∵点C与点B关于x轴对称， ∴C（0，﹣3），

设直线O′C的解析式为y=kx+b，

把O′（），C（0，﹣3）代入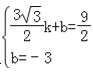得，解得，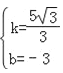

∴直线O′C的解析式为y=x﹣3， 当y=0时，x﹣3=0，解得x=，则P（，0），

∴OP=， ∴O′P′=OP=， 作P′D⊥O′H于D，

∵∠BO′A=∠BOA=90°，∠BO′H=30°， ∴∠DP′O′=30°，

∴O′D=O′P′=，P′D=， ∴DH=O′H﹣O′，

∴P′点的坐标为（，）．