题目内容
【题目】【问题提出】
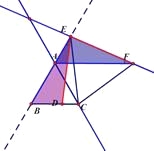
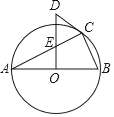
如图①,已知△ABC是等腰三角形,点E在线段AB上,点D在直线BC上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF连接EF
试证明:AB=DB+AF
【类比探究】
(1)如图②,如果点E在线段AB的延长线上,其他条件不变,线段AB,DB,AF之间又有怎样的数量关系?请说明理由
(2)如果点E在线段BA的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB,DB,AF之间的数量关系,不必说明理由.
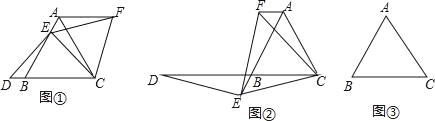
【答案】证明见解析;(1)AB=BD﹣AF;(2)AF=AB+BD.
【解析】试题分析:(1)根据旋转的性质得出△EDB与FEA全等的条件BE=AF,再结合已知条件和旋转的性质推出∠D=∠AEF,∠EBD=∠EAF=120°,得出△EDB≌FEA,所以BD=AF,等量代换即可得出结论.(2)先画出图形证明∴△DEB≌△EFA,方法类似于(1);(3)画出图形根据图形直接写出结论即可.
试题解析:(1)证明:DE=CE=CF,△BCE
由旋转60°得△ACF,
∴∠ECF=60°,BE=AF,CE=CF,
∴△CEF是等边三角形,
∴EF=CE,
∴DE=EF,∠CAF=∠BAC=60°,
∴∠EAF=∠BAC+∠CAF=120°,
∵∠DBE=120°,
∴∠EAF=∠DBE,
又∵A,E,C,F四点共圆,
∴∠AEF=∠ACF,
又∵ED=DC,
∴∠D=∠BCE,∠BCE=∠ACF,
∴∠D=∠AEF,
∴△EDB≌FEA,
∴BD=AF,AB=AE+BF,
∴AB=BD+AF.
类比探究(1)DE=CE=CF,△BCE由旋转60°得△ACF,
∴∠ECF=60°,BE=AF,CE=CF,
∴△CEF是等边三角形,
∴EF=CE,
∴DE=EF,∠EFC=∠BAC=60°,
∠EFC=∠FGC+∠FCG,∠BAC=∠FGC+∠FEA,
∴∠FCG=∠FEA,
又∠FCG=∠EAD
∠D=∠EAD,
∴∠D=∠FEA,
由旋转知∠CBE=∠CAF=120°,
∴∠DBE=∠FAE=60°
∴△DEB≌△EFA,
∴BD=AE, EB=AF,
∴BD=FA+AB.
即AB=BD-AF.
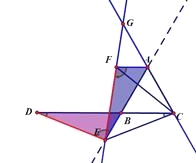
(2)AF=BD+AB(或AB=AF-BD)