题目内容
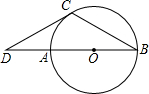
PA，PB与⊙O分别相切于点A，B，点C为⊙O上异于A，B的一点，若∠P=70°，则∠ACB=______．
连接OA、OB．
∵PA，PB分别切⊙O于点A，B，
∴OA⊥PA，OB⊥PB；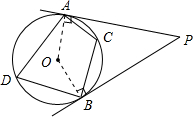
∴∠PAO=∠PBO=90°；
又∵∠APB=70°，
∴在四边形AOBP中，∠AOB=360°-90°-90°-70°=110°，
∴∠ADB=
×∠AOB=
×110°=55°，
即当C在D处时，∠ACB=55°．
在四边形ADBC中，∠ACB=180°-∠ADB=180°-55°=125°．
于是∠ACB的度数为55°或125°，
故答案为：55°或125°．
∵PA，PB分别切⊙O于点A，B，
∴OA⊥PA，OB⊥PB；
∴∠PAO=∠PBO=90°；又∵∠APB=70°，
∴在四边形AOBP中，∠AOB=360°-90°-90°-70°=110°，
∴∠ADB=
| 1 |
| 2 |
| 1 |
| 2 |
即当C在D处时，∠ACB=55°．
在四边形ADBC中，∠ACB=180°-∠ADB=180°-55°=125°．
于是∠ACB的度数为55°或125°，
故答案为：55°或125°．
练习册系列答案
尖子生新课堂课时作业系列答案
相关题目
