Question

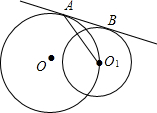
如图1，已知⊙O和⊙O′都经过点A和点B，直线PQ切⊙O于点P，交⊙O′于点Q、M，交AB的延长线于点N．
（1）求证：PN²=NM•NQ．
（2）若M是PQ的中点，设MQ=x，MN=y，求证：x=3y．
（3）若⊙O′不动，把⊙O向右或向左平移，分别得到图2、图3、图4，请你判断（直接写出判断结论，不需证明）：
①（1）题结论是否仍然成立？
②在图2中，（2）题结论是否仍然成立？
在图3、图4中，若将（2）题条件改为：M是PN的中点，设MQ=x，MN=y，则x=3y的结论是否仍然成立？

Answer 1

（1）证明：∵PQ切⊙O于P，
∴PN²=NB•NA，
∵NB•NA=NM•NQ，
∴PN²=NM•NQ；

（2）证明：∵PM=MQ=x，MN=y，PN²=NM•NQ，
∴（x-y）²=y（x+y），
整理，得x²=3xy，
∵x≠0，
∴x=3y；

（3）①在图2、图3、图4中（1）题结论都成立．
②在图2中（2）题结论成立．在图3、图4中，按题意改变条件后，x=3y的结论仍然成立．