题目内容
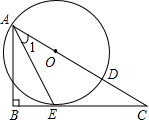
如图，已知点O为Rt△ABC斜边AC上一点，以点O为圆心，OA长为半径的⊙O与BC相切于点E，与AC相交于点D，连接AE．
（1）求证：AE平分∠CAB；
（2）探求图中∠1与∠C的数量关系，并求当AE=EC时tanC的值．
（1）求证：AE平分∠CAB；
（2）探求图中∠1与∠C的数量关系，并求当AE=EC时tanC的值．
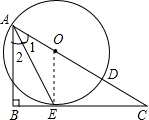
（1）证明：连接OE，
∵⊙O与BC相切于点E，
∴OE⊥BC，
∵AB⊥BC，
∴AB∥OE，
∴∠2=∠AEO，
∵OA=OE，
∴∠1=∠AEO，
∴∠1=∠2，即AE平分∠CAB；
（2）∠C=90°-2∠1，tanC=
．
∵∠EOC是△AOE的外角，
∴∠1+∠AEO=∠EOC，
∵∠1=∠AEO，∠OEC=90°，
∴∠C=90°-2∠1，
当AE=CE时，∠1=∠C，
∵2∠1+∠C=90°
∴3∠C=90°，∠C=30°
∴tanC=tan30°=
．
∵⊙O与BC相切于点E，
∴OE⊥BC，
∵AB⊥BC，
∴AB∥OE，
∴∠2=∠AEO，
∵OA=OE，
∴∠1=∠AEO，
∴∠1=∠2，即AE平分∠CAB；
（2）∠C=90°-2∠1，tanC=
| ||
| 3 |
∵∠EOC是△AOE的外角，
∴∠1+∠AEO=∠EOC，
∵∠1=∠AEO，∠OEC=90°，
∴∠C=90°-2∠1，
当AE=CE时，∠1=∠C，
∵2∠1+∠C=90°
∴3∠C=90°，∠C=30°
∴tanC=tan30°=
| ||
| 3 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
