Question

【题目】如图，矩形ABCD中，AB=2，AD=4，动点E在边BC上，与点B、C不重合，过点A作DE的垂线，交直线CD于点F．设DF=x，EC=y．

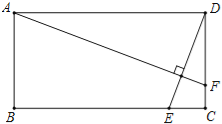
（1）求y关于x的函数关系式，并写出x的取值范围．

（2）当CF=1时，求EC的长．

（3）若直线AF与线段BC延长线交于点G，当△DBE与△DFG相似时，求DF的长．

Answer 1

【答案】（1），（0＜x＜8）；（2）EC的长为或；（3）DF的长为或．

【解析】

试题（1）易证△ADF∽△DCE，然后运用相似三角形的性质即可得到y与x的关系，然后根据y的范围就可得到x的范围；

（2）由于点F的位置不确定，需分点F在线段DC及点F在线段DC的延长线上两种情况进行讨论，然后利用y与x的关系即可解决问题；

（3）由∠DEC=∠AFD=90﹣∠EDC可得∠BED=∠DFG，因而在△DBE和△DFG中，点E与点F是对应点，故当△DBE与△DFG相似时，可分△DEB∽△GFD和△DEB∽△DFG两种情况进行讨论，然后只需用x的代数式表示ED、FG、EB，再运用相似三角形的性质即可解决问题．

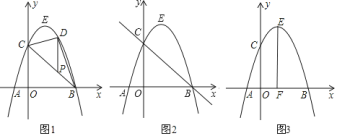
试题解析：（1）如图1，

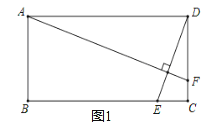
∵四边形ABCD是矩形，

∴DC=AB=2，∠ADC=∠BCD=90°．

又∵AF⊥DE，

∴∠ADF=∠DCE=90°，∠DAF=∠EDC=90°﹣∠DFA，

∴△ADF∽△DCE，

∴，

∴，即．

∵点E在线段BC上，与点B、C不重合，

∴0＜y＜4，∴0＜＜4，即0＜x＜8，

∴，（0＜x＜8）；

（2）①当点F线段DC上时，

∵CF=1，

∴DF=x=2﹣1=1，此时CE=y=x=；

②当点F线段DC延长线上时，

∵CF=1，

∴DF=x=2+1=3，此时CE=y=x=；

∴当CF=1时，EC的长为或；

（3）在Rt△ADF中，AF=，

在Rt△DCE中，DE=，

∵四边形ABCD是矩形，

∴AD∥BC，

∴△ADF∽△GCF，

∴，

∴FG=．

∵∠DEC=∠AFD=90﹣∠EDC，

∴∠BED=∠DFG，

∴当△DBE与△DFG相似时，可分以下两种情况讨论：

①△DEB∽△GFD，如图2，

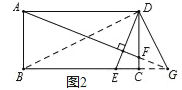
则有，

∴EDFD=FGEB，

∴（4﹣x），

解得：x=．

②若△DEB∽△DFG，如图3，

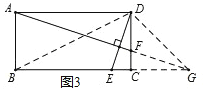
则有，

∴EDFG=EBFD，

∴（4﹣x），

整理得：3x2+8x﹣16=0，

解得：x1=，x2=﹣4（舍去）．

综上所述：DF的长为或．