题目内容
【题目】已知抛物线的表达式为![]() .
.
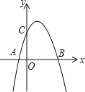
![]() 求此抛物线与
求此抛物线与![]() 轴、
轴、![]() 轴的交点坐标;
轴的交点坐标;
![]() 求抛物线与坐标轴围成的三角形的面积;
求抛物线与坐标轴围成的三角形的面积;
![]() 在上述的抛物线上是否存在这样的点
在上述的抛物线上是否存在这样的点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 点的坐标.
点的坐标.
![]() 在上述的抛物线上是否存在这样的点
在上述的抛物线上是否存在这样的点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 点的坐标.
点的坐标.
![]() 在上述的抛物线上是否存在这样的点
在上述的抛物线上是否存在这样的点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 点的坐标.
点的坐标.
【答案】(1)![]() 点坐标为
点坐标为![]() ,
,![]() ,
,![]() ;(2)6;(3)存在,点
;(2)6;(3)存在,点![]() 坐标为
坐标为![]() ;(4)存在,点
;(4)存在,点![]() 坐标为
坐标为![]() ;(5)不存在,理由详见解析.
;(5)不存在,理由详见解析.
【解析】
(1)当x=0时可求得点C坐标,当y=0时可求得点A,B坐标,即可解题;
(2)根据A,B坐标可以求得AB长度,根据C点坐标可以求得OC长度,即可解题;
(3)存在,根据S△ABP=S△ABC可得点P纵坐标与点C纵坐标相等,且为3,即可求得点P坐标;
(4)存在,根据S△ABP=S△ABC可得点P纵坐标为4,即可求得点P坐标;
(5)不存在,根据S△ABP=![]() S△ABC可得点P纵坐标为5,方程无解,故不存在.
S△ABC可得点P纵坐标为5,方程无解,故不存在.
![]() 当
当![]() 时,
时,![]() ,
,
∴![]() 点坐标为
点坐标为![]() ,
,
当![]() 时,
时,![]() ,整理得:
,整理得:![]() ,
,
解得:![]() 或
或![]() ,
,
∵![]() 点在
点在![]() 点左侧,
点左侧,
∴![]() ,
,![]() ;
;
![]() ∴
∴![]() ;
;
![]() 存在,
存在,
∵![]() ,
,
∴点![]() 纵坐标与点
纵坐标与点![]() 纵坐标相等,且为
纵坐标相等,且为![]() ,
,
∴![]() ,
,
解得:![]() 或
或![]() ,∴点
,∴点![]() 坐标为
坐标为![]() ;
;
![]() 存在,
存在,
∵![]() ,
,
∴点![]() 纵坐标为点
纵坐标为点![]() 纵坐标
纵坐标![]() 倍,即为
倍,即为![]() ,
,
∴![]() ,
,
解得:![]() ,∴点
,∴点![]() 坐标为
坐标为![]() ;
;
![]() 不存在,
不存在,
∵![]() ,
,
∴点![]() 纵坐标为点
纵坐标为点![]() 纵坐标
纵坐标![]() 倍,即为
倍,即为![]() ,
,
∴![]() ,
,
解得:![]() 无解,∴不存在点
无解,∴不存在点![]() .
.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
【题目】近年来“哈罗单车”和“哈啰助力车”在街头流行.随着市民对这两种车的使用率的提升,经营“哈罗单车”和“哈啰助力车”的两家公司也有了越来越高的收人.初三某班的实践小组对两家公司近10个周的收入进行了调查,就收入(单位:千元)情况制作了如下的统计图:

根据以上信息,整理分析数据如下:
公司 | 平均周收入/千元 | 周收入中位数/千元 | 周收入众数/千元 | 方差 |
哈罗单车 | _____ | 6 | 6 | 1.2 |
哈啰助力车 | 6 | _____ | 4 | _____ |
(1)完成表格填空;
(2)“哈罗单车”和“哈啰助力车”在该地各有500辆和300辆.从收入的情况看,上个周这2家公司都达到了近10个周的最高收人.已知每骑用一次“哈罗单车”和“哈啰助力车”,公司就分别收人1元和2元,通过计算在上周每辆车的周平均骑用次数,说明哪种车比较抢手?