题目内容
【题目】已知抛物线![]() 的图象经过点
的图象经过点![]() 、
、![]() ,顶点为
,顶点为![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
![]() 求抛物线的解析式和顶点
求抛物线的解析式和顶点![]() 的坐标;
的坐标;
![]() 如图
如图![]() ,
,![]() 为线段
为线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴平行线,交抛物线于点
轴平行线,交抛物线于点![]() ,当
,当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
![]() 如图
如图![]() ,若点
,若点![]() 是直线
是直线![]() 上的动点,点
上的动点,点![]() 、
、![]() 、
、![]() 所构成的三角形与
所构成的三角形与![]() 相似,请直接写出所有点
相似,请直接写出所有点![]() 的坐标;
的坐标;
![]() 如图
如图![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() 点,
点,![]() 是
是![]() 轴上一动点,
轴上一动点,![]() 是线段
是线段![]() 上一点,若
上一点,若![]() ,则
,则![]() 的最大值为________,最小值为________.
的最大值为________,最小值为________.
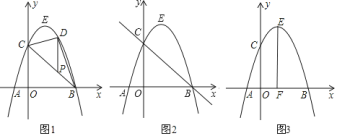
【答案】(1)抛物线解析式为y=x2+2x+3,顶点坐标E(1,4).(2)P(![]() ,
,![]() ).(3)Q点坐标为(3,0),(3,6), (
).(3)Q点坐标为(3,0),(3,6), (![]() ,
,![]() ),(
),(![]() ,
,![]() ).(4)m的最大值为5,最小值为54.
).(4)m的最大值为5,最小值为54.
【解析】
(1)利用待定系数法,把A、B两点坐标代入抛物线的解析式,转化为解方程组即可.
(2)设P(a,3-a),则D(a,-a2+2a+3),根据S△BDC=S△PDC+S△PDB,构建二次函数,利用二次函数的性质解决即可.
(3)根据相似三角形性质和判定,分类讨论.
(4)首先过C作CH⊥EF于H点,则CH=EH=1,然后分别从点M在EF左侧与M在EF右侧时去分析求解即可求得答案.
(1)∵抛物线y=x2+bx+c的图象经过点A(1,0)、B(3,0),
∴![]() ,
,
解得![]() ,
,
∴抛物线解析式为y=x2+2x+3,
顶点坐标E(1,4).
(2)如图1中,
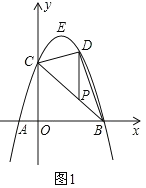
∵B(3,0),C(0,3)
∴直线BC的解析式为y=x+3,
设P(a,3a),则D(a,a2+2a+3),
∴PD=(a2+2a+3)(3a)=a2+3a,
∴S△BDC=S△PDC+S△PDB=![]()
PDa+![]() PD(3a)=
PD(3a)=![]() PD3,
PD3,
=![]() (a2+3a)=
(a2+3a)=![]() (a
(a![]() )2+
)2+![]() ,
,
∵![]() <0,
<0,
∴当a=时,△BDC的面积最大,此时P(
![]() ,
,![]() ).
).
(3)如图2中,
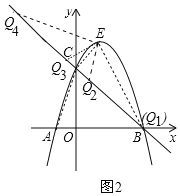
∵C(0,3),E(1,4),B(3,0),
∴直线EC的解析式为y=x+3,直线BC的解析式为y=x+3,
∵1×(1)=1,
∴EC⊥BC,
∴∠ECB=90,
∴当![]() 或
或![]() 时,点Q、C、E所构成的三角形与△AOC相似,
时,点Q、C、E所构成的三角形与△AOC相似,
即![]() =
=![]() 或
或![]() =
=![]() ,
,
∴CQ=![]() 或3
或3![]() ,
,
∴Q1(3,0),Q2(![]() ,
,![]() ),
),
根据对称性可知当Q3(![]() ,
,![]() ),Q4(3,6)时也满足条件,
),Q4(3,6)时也满足条件,
综上所述,Q点坐标为(3,0),(3,6), (![]() ,
,![]() ),(
),(![]() ,
,![]() ).
).
(4)如图3中,过C作CH⊥EF于H点,则CH=EH=1,
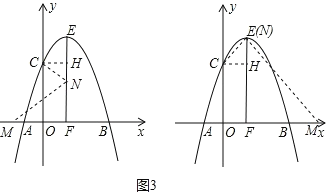
当M在EF左侧时,
∵∠MNC=90,
则△MNF∽△NCH,
∴![]() ,
,
设FN=n,则NH=3n,
∴![]() ,
,
即n23nm+1=0,
关于n的方程有解,△=(3)24(m+1)0,
得m54,
当M在EF右侧时,Rt△CHE中,CH=EH=1,∠CEH=45,即∠CEF=45,
作EM⊥CE交x轴于点M,则∠FEM=45,
∵FM=EF=4,
∴OM=5,
即N为点E时,OM=5,此时m的值最大,
∴m5,
∴m的最大值为5,最小值为54,

 阅读快车系列答案
阅读快车系列答案【题目】近年来“哈罗单车”和“哈啰助力车”在街头流行.随着市民对这两种车的使用率的提升,经营“哈罗单车”和“哈啰助力车”的两家公司也有了越来越高的收人.初三某班的实践小组对两家公司近10个周的收入进行了调查,就收入(单位:千元)情况制作了如下的统计图:

根据以上信息,整理分析数据如下:
公司 | 平均周收入/千元 | 周收入中位数/千元 | 周收入众数/千元 | 方差 |
哈罗单车 | _____ | 6 | 6 | 1.2 |
哈啰助力车 | 6 | _____ | 4 | _____ |
(1)完成表格填空;
(2)“哈罗单车”和“哈啰助力车”在该地各有500辆和300辆.从收入的情况看,上个周这2家公司都达到了近10个周的最高收人.已知每骑用一次“哈罗单车”和“哈啰助力车”,公司就分别收人1元和2元,通过计算在上周每辆车的周平均骑用次数,说明哪种车比较抢手?