题目内容
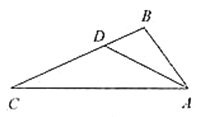
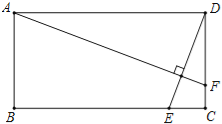
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径是2cm,E是弧AD的中点,求阴影部分的面积(结果保留π和根号)
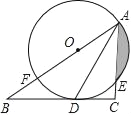
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OD,只要证明OD∥AC即可解决问题;
(2)连接OE,OE交AD于K.只要证明△AOE是等边三角形即可解决问题.
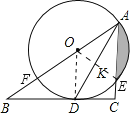
(1)连接OD.
 、
、
∵OA=OD,
∴∠OAD=∠ODA,
∵∠OAD=∠DAC,
∴∠ODA=∠DAC,
∴OD∥AC,
∴∠ODB=∠C=90°,
∴OD⊥BC,
∴BC是⊙O的切线.
(2)连接OE,OE交AD于K.
∵![]() ,
,
∴OE⊥AD,
∵∠OAK=∠EAK,AK=AK,∠AKO=∠AKE=90°,
∴△AKO≌△AKE,
∴AO=AE=OE,
∴△AOE是等边三角形,
∴∠AOE=60°,
∴S阴=S扇形OAE-S△AOE=![]() ×22=
×22=![]() .
.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案【题目】近年来“哈罗单车”和“哈啰助力车”在街头流行.随着市民对这两种车的使用率的提升,经营“哈罗单车”和“哈啰助力车”的两家公司也有了越来越高的收人.初三某班的实践小组对两家公司近10个周的收入进行了调查,就收入(单位:千元)情况制作了如下的统计图:

根据以上信息,整理分析数据如下:
公司 | 平均周收入/千元 | 周收入中位数/千元 | 周收入众数/千元 | 方差 |
哈罗单车 | _____ | 6 | 6 | 1.2 |
哈啰助力车 | 6 | _____ | 4 | _____ |
(1)完成表格填空;
(2)“哈罗单车”和“哈啰助力车”在该地各有500辆和300辆.从收入的情况看,上个周这2家公司都达到了近10个周的最高收人.已知每骑用一次“哈罗单车”和“哈啰助力车”,公司就分别收人1元和2元,通过计算在上周每辆车的周平均骑用次数,说明哪种车比较抢手?