Question

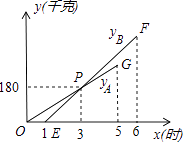
【题目】二次函数y=ax2+bx+c的图象如图所示，下列结论：
①4ac＜b2；②a+c＞b；③2a+b＞0．
其中正确的有（ ）

A.①②
B.①③
C.②③
D.①②③

Answer 1

【答案】B
【解析】∵抛物线与x轴有两个交点，

∴△＞0，

∴b2﹣4ac＞0，

∴4ac＜b2，故①正确，

∵x=﹣1时，y＜0，

∴a﹣b+c＜0，

∴a+c＜b，故②错误，

∴对称轴x＞1，a＜0，

∴﹣ ＞1，

∴﹣b＜2a，

∴2a+b＞0，故③正确．

所以答案是：B．

【考点精析】根据题目的已知条件，利用二次函数图象以及系数a、b、c的关系的相关知识可以得到问题的答案，需要掌握二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）．