题目内容
【题目】某物流公司引进A、B两种机器人用来搬运某种货物，这两种机器人充满电后可以连续搬运5小时，A种机器人于某日0时开始搬运，过了1小时，B种机器人也开始搬运，如图，线段OG表示A种机器人的搬运量yA（千克）与时间x（时）的函数图象，线段EF表示B种机器人的搬运量yB（千克）与时间x（时）的函数图象．根据图象提供的信息，解答下列问题：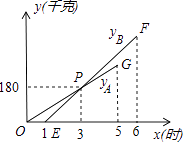
（1）求yB关于x的函数解析式；
（2）如果A、B两种机器人连续搬运5个小时，那么B种机器人比A种机器人多搬运了多少千克？
【答案】
（1）解：设yB关于x的函数解析式为yB=kx+b（k≠0）．
将点（1，0）、（3，180）代入得： 
，
解得：k=90，b=﹣90．
所以yB关于x的函数解析式为yB=90x﹣90（1≤x≤6）
（2）解：设yA关于x的解析式为yA=k1x．
根据题意得：3k1=180．
解得：k1=60．
所以yA=60x．
当x=5时，yA=60×5=300（千克）；
x=6时，yB=90×6﹣90=450（千克）．
450﹣300=150（千克）．
答：如果A、B两种机器人各连续搬运5小时，B种机器人比A种机器人多搬运了150千克．
【解析】（1）设yB关于x的函数解析式为yB=kx+b（k≠0），再待定系数法可求得函数的解析式；
（2）设yA关于x的解析式为yA=k1x．待定系数法求得yA关于x的解析式，然后将x=6，x=5代入一次函数和正比例函数的解析式求得yA，yB的值，最后求得yA与yB的差即可得到答案．
阅读快车系列答案【题目】请你用学习“一次函数”时积累的经验和方法研究函数
的图象和性质，并解决问题．
完成下列步骤，画出函数的图象；
列表、填空；
x |
|
|
|
| 0 | 1 | 2 | 3 |
|
y |
| 3 | ______ | 1 | ______ | 1 | 2 | 3 |
|
描点：
连线
观察图象，当x______时，y随x的增大而增大；
结合图象，不等式
的解集为______．
