Question

【题目】（1）如图（1），在△ABC 中，∠BAC=70°，点 D 在 BC 的延长线上，三角形的内角∠ABC 与外角∠ACD 的角平分线 BP，CP 相交于点 P，求∠P 的度数.（写出完整的解答过程）

（感知）：图（1）中，若∠BAC=m°，那么∠P= °（用含有 m 的代数式表示）

（探究）：如图（2）在四边形 MNCB 中，设∠M=α，∠N＝β，α+β＞180°，四边形的内角∠MBC与外角∠NCD 的角平分线 BP，CP 相交于点 P.为了探究∠P 的度数与 α 和 β 的关系，小明同学想到将这个问题转化图（1）的模型，因此，他延长了边 BM 与 CN，设它们的交点为点 A， 如图（ 3 ）， 则∠ A= （用含有 α 和 β 的代数式表示）， 因此∠P= ．（用含有 α 和 β 的代数式表示）

（拓展）：将（2）中的 α+β＞180°改为 α+β＜180°，四边形的内角∠MBC 与外角∠NCD 的角平分线所在的直线相交于点 P，其它条件不变，请直接写出∠P＝ 　　．（用 α，β的代数式表示）

Answer 1

【答案】（1）35°；感知：m°，探究：α+β-180°，（α+β）-90°；拓展：90°-α-β

【解析】

（1）根据角平分线的定义可得∠CBP=∠ABC，根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义表示出∠DCP，然后整理即可得到∠P=∠A，代入数据计算即可得解．

[感知]求∠P度数的方法同（1）

[探究] 添加辅助线，利用（1）中结论解决问题即可；根据四边形的内角和定理表示出∠BCN，再表示出∠DCN，然后根据角平分线的定义可得∠PBC=∠ABC，∠PCD=∠DCN，三角形的一个外角等于与它不相邻的两个内角的和可得∠P+∠PBC=∠PCD，然后整理即可得解；

拓展：同探究的思路求解即可

（1）∵BP平分∠ABC，

∴∠CBP=∠ABC，

∵CP平分△ABC的外角，

∴∠DCP=∠ACD=（∠A+∠ABC）=∠A+∠ABC，

在△BCP中，由三角形的外角性质，∠DCP=∠CBP+∠P=∠ABC+∠P，

∴∠A+∠ABC=∠ABC+∠P，

∴∠P=∠A=×70°=35°．

感知：由（1）知∠P=∠A

∵∠BAC=m°，

∴∠P=m°，

故答案为：m°，

探究：延长BM交CN的延长线于A．

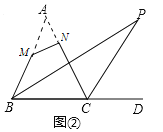
∵∠A=180°-∠AMN-∠ANM=180°-（180°-α）-（180°-β）=α+β-180°，

由（1）可知：∠P=∠A，

∴∠P=（α+β）-90°；

故答案为：α+β-180°，（α+β）-90°；

[拓展] 如图③，延长MB交NC的延长线于A．

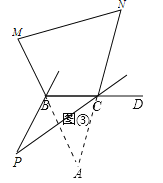
∵∠A=180°-α-β，∠P=∠A，

∴∠P=（180°-α-β）=90°-α-β

故答案为：90°-α-β