题目内容
如图，直线x=t（t＞0）与反比例函数
的图象分别交于B、C两点，A为y轴上的任意一点，则△ABC的面积为（ ）
A．3 B．
C．
D．不能确定
的图象分别交于B、C两点，A为y轴上的任意一点，则△ABC的面积为（ ）A．3 B．
C． D．不能确定C
试题分析：先分别求出B、C两点的坐标，得到BC的长度，再根据三角形的面积公式即可得出△ABC的面积．
解：把x=t分别代入
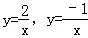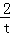，得y=
，y=﹣
，所以B（t，
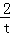）、C（t，﹣
），所以BC=
﹣（﹣）=
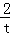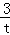．∵A为y轴上的任意一点，
∴点A到直线BC的距离为t，
∴△ABC的面积=
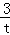××t=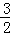
．故选C．
点评：此题考查了反比例函数图象上点的坐标特征及三角形的面积，求出BC的长度是解答本题的关键，难度一般．
练习册系列答案
相关题目
上，B、D在双曲线y2=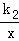
上，k1=2k2（k1＞0），AB∥y轴，S?ABCD=24，则k1= ．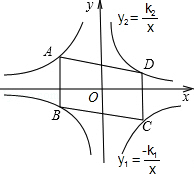
（x＜0）的图象于B，交函数
（x＞0）的图象于C，则线段AB与线段AC的长度之比为 _________ ．
；
．
与一次函数y2=﹣x+b的图象交于点A（2，3）和点B（m，2）．由图象可知，对于同一个x，若y1＞y2，则x的取值范围是 _________ ．
经过点A(1，0)，与双曲线
交于点B(2，1)．过点P(
，
轴的平行线分别交双曲线
于点M、N．
的值；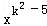
是反比例函数，则k= ．
交OB于D，且OD：DB=1：2，若△OBC的面积等于3，则k的值（ ）
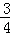
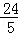
的对称性叙述错误的是（ ）