题目内容
如图,平行四边形ABCD的顶点A、C在双曲线y1=﹣ 上,B、D在双曲线y2=
上,B、D在双曲线y2=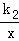 上,k1=2k2(k1>0),AB∥y轴,S?ABCD=24,则k1= .
上,k1=2k2(k1>0),AB∥y轴,S?ABCD=24,则k1= .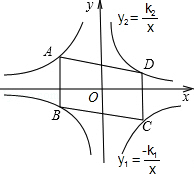
 上,B、D在双曲线y2=
上,B、D在双曲线y2=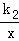 上,k1=2k2(k1>0),AB∥y轴,S?ABCD=24,则k1= .
上,k1=2k2(k1>0),AB∥y轴,S?ABCD=24,则k1= .
8
试题分析:利用平行四边形的性质设A(x,y1)、B(x、y2),根据反比例函数的图象关于原点对称的性可知C(﹣x,﹣y1)、D(﹣x、﹣y2);然后由反比例函数图象上点的坐标特征,将点A、B的坐标分别代入它们所在的函数图象的解析式,求得y1=﹣2y2;最后根据S?ABCD=
 •|2x|=24可以求得k2=y2x=4.
•|2x|=24可以求得k2=y2x=4.解:在?ABCD中,AB∥CD,AB=CD(平行四边形的对应边平行且相等),故设A(x,y1)、B(x、y2),则根据反比例函数的图象关于原点对称的性质知,C(﹣x,﹣y1)、D(﹣x、﹣y2).

∵A在双曲线y1=﹣
 上,B在双曲线y2=
上,B在双曲线y2=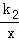 上,
上,∴x=﹣
 ,x=
,x= ,
,∴﹣
 =
= ;
;又∵k1=2k2(k1>0),
∴y1=﹣2y2;
∵S?ABCD=24,
∴
 •|2x|=6|y2x|=24,
•|2x|=6|y2x|=24,解得,y2x=±4,
∵双曲线y2=
 位于第一、三象限,
位于第一、三象限,∴k2=4,
∴k1=2k2=8
故答案是:8.
点评:本题考查了反比例函数综合题.根据反比例函数的图象关于原点对称的性质求得点A与点B的纵坐标的数量关系是解答此题的难点.

练习册系列答案
相关题目
 是反比例函数,则k必须满足( )
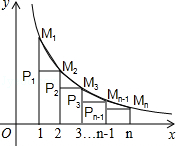
是反比例函数,则k必须满足( )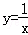 的图象,当x取1,2,3,…,n时,对应在反比例图象上的点分别为M1,M2,M3…,Mn,则
的图象,当x取1,2,3,…,n时,对应在反比例图象上的点分别为M1,M2,M3…,Mn,则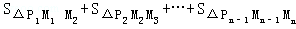 = .
= .
 的图象向右平移1个单位,所得图象的函数表达式为 _________ ,再向上平移1个单位,所得图象的函数表达式为 _________ ;
的图象向右平移1个单位,所得图象的函数表达式为 _________ ,再向上平移1个单位,所得图象的函数表达式为 _________ ; 的图象可由y=
的图象可由y= 的图象向 _________ 平移 _________ 个单位得到;y=
的图象向 _________ 平移 _________ 个单位得到;y= 的图象可由哪个反比例函数的图象经过怎样的变换得到;
的图象可由哪个反比例函数的图象经过怎样的变换得到; (ab≠0,且a≠b)的图象可由哪个反比例函数的图象经过怎样的变换得到?
(ab≠0,且a≠b)的图象可由哪个反比例函数的图象经过怎样的变换得到?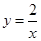 (
(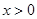 )图象上任意一点,MN⊥y轴于N,点P是x轴上的动点,则△MNP的面积为( )
)图象上任意一点,MN⊥y轴于N,点P是x轴上的动点,则△MNP的面积为( )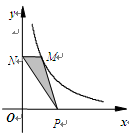
 x+2与坐标轴交于A、B两点,与双曲线y=
x+2与坐标轴交于A、B两点,与双曲线y= 交于点C,A、D关于y轴对称,若S四边形OBCD=6,则k= .
交于点C,A、D关于y轴对称,若S四边形OBCD=6,则k= .
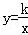 (k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若
(k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若 (m为大于l的常数).记△CEF的面积为S1,△OEF的面积为S2,则
(m为大于l的常数).记△CEF的面积为S1,△OEF的面积为S2,则 = . (用含m的代数式表示)
= . (用含m的代数式表示)
 的图象分别交于B、C两点,A为y轴上的任意一点,则△ABC的面积为( )
的图象分别交于B、C两点,A为y轴上的任意一点,则△ABC的面积为( )
 C.
C. D.不能确定
D.不能确定 ,
, 在第一象限内的图象,如图,点P1,P2,P3,…,P2005在反比例函数
在第一象限内的图象,如图,点P1,P2,P3,…,P2005在反比例函数