题目内容
如图,已知梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,过点C的双曲线 交OB于D,且OD:DB=1:2,若△OBC的面积等于3,则k的值( )
交OB于D,且OD:DB=1:2,若△OBC的面积等于3,则k的值( )

 交OB于D,且OD:DB=1:2,若△OBC的面积等于3,则k的值( )
交OB于D,且OD:DB=1:2,若△OBC的面积等于3,则k的值( )
| A.等于2 | B.等于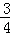 | C.等于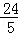 | D.无法确定 |
B
试题分析:先设出B点坐标,即可表示出C点坐标,根据三角形的面积公式和反比例函数的几何意义即可解答.
解:方法1:设B点坐标为(a,b),
∵OD:DB=1:2,
∴D点坐标为(
 a,
a, b),
b),根据反比例函数的几何意义,
∴
 a•
a• b=k,
b=k,∴ab=9k①,
∵BC∥AO,AB⊥AO,C在反比例函数y=
 的图象上,
的图象上,∴设C点横坐标为m,
则C点坐标为(m,b)
将(m,b)代入y=
 得,
得,m=
 ,
,BC=a﹣
 ,
,又因为△OBC的高为AB,
所以S△OBC=
 (a﹣
(a﹣ )•b=3,
)•b=3,所以
 (a﹣
(a﹣ )•b=3,
)•b=3,(a﹣
 )b=6,
)b=6,ab﹣k=6②,
把①代入②得,
9k﹣k=6,
解得k=
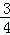 .
.方法2:延长BC交y轴于E,过D作x轴的垂线,垂足为F.
由△OAB的面积=△OBE的面积,△ODF的面积=△OCE的面积,
可知,△ODF的面积=
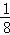 梯形DFAB=
梯形DFAB=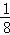 △BOC的面积=
△BOC的面积= ,
,即
 k=
k= ,
,k=
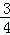 .
.故选B.

点评:本题考查了反比例系数k的几何意义.此题还可这样理解:当满足OD:DB=1:2时,当D在函数图象上运动时,面积为定值.

练习册系列答案
相关题目
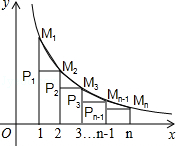
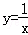 的图象,当x取1,2,3,…,n时,对应在反比例图象上的点分别为M1,M2,M3…,Mn,则
的图象,当x取1,2,3,…,n时,对应在反比例图象上的点分别为M1,M2,M3…,Mn,则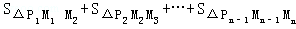 = .
= .
 的图象向右平移1个单位,所得图象的函数表达式为 _________ ,再向上平移1个单位,所得图象的函数表达式为 _________ ;
的图象向右平移1个单位,所得图象的函数表达式为 _________ ,再向上平移1个单位,所得图象的函数表达式为 _________ ; 的图象可由y=
的图象可由y= 的图象向 _________ 平移 _________ 个单位得到;y=
的图象向 _________ 平移 _________ 个单位得到;y= 的图象可由哪个反比例函数的图象经过怎样的变换得到;
的图象可由哪个反比例函数的图象经过怎样的变换得到; (ab≠0,且a≠b)的图象可由哪个反比例函数的图象经过怎样的变换得到?
(ab≠0,且a≠b)的图象可由哪个反比例函数的图象经过怎样的变换得到? 关于y轴对称的函数的解析式为 .
关于y轴对称的函数的解析式为 . (k≠0)关于x轴对称的函数的解析式.
(k≠0)关于x轴对称的函数的解析式. ,若用x表示y,则y= .
,若用x表示y,则y= . (x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5,并设其面积分别为S1、S2、S3、S4、S5,则S1+S2+S3+S4+S5的值为( )
(x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5,并设其面积分别为S1、S2、S3、S4、S5,则S1+S2+S3+S4+S5的值为( )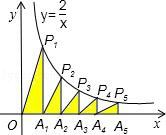
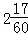

 的图象分别交于B、C两点,A为y轴上的任意一点,则△ABC的面积为( )
的图象分别交于B、C两点,A为y轴上的任意一点,则△ABC的面积为( )
 C.
C. D.不能确定
D.不能确定 (
( <0)的图象上,则x1,x2,x3从小到大排列为 (用“<”号连接).
<0)的图象上,则x1,x2,x3从小到大排列为 (用“<”号连接).