题目内容
【题目】如图,已知P为锐角∠MAN内部一点,过点P作PB⊥AM于点B,PC⊥AN于点C,以PB为直径作⊙O,交直线CP于点D,连接AP,BD,AP交⊙O于点E.

(1)求证:∠BPD=∠BAC.
(2)连接EB,ED,当tan∠MAN=2,AB=2![]() 时,在点P的整个运动过程中.
时,在点P的整个运动过程中.
①若∠BDE=45°,求PD的长;
②若△BED为等腰三角形,求所有满足条件的BD的长;
(3)连接OC,EC,OC交AP于点F,当tan∠MAN=1,OC//BE时,记△OFP的面积为S1,△CFE的面积为S2,请写出![]() 的值.
的值.
【答案】(1)证明见解析;(2)①PD=2;当BD为2,3或![]() 时,△BDE为等腰三角形;(3)
时,△BDE为等腰三角形;(3)![]() =
=![]()
【解析】
分析: (1)根据垂直的定义得出∠ABP=∠ACP=90°,根据四边形的内角和得出∠BAC+∠BPC=180°,根据平角的定义得出∠BPD+∠BPC=180°,根据同角的余角相等得出∠BPD=∠BAC ;
(2)①如图1,根据等腰直角三角形的性质得出BP=AB=2![]() , 根据等角的同名三角函数值相等及正切函数的定义得出BP=
, 根据等角的同名三角函数值相等及正切函数的定义得出BP=![]() PD,从而得出PD的长;②Ⅰ如图2,当BD=BE时,∠BED=∠BDE,故∠BPD=∠BPE=∠BAC根据等角的同名三角函数值相等得出tan∠BPE=2,根据正切函数的定义由AB=2
PD,从而得出PD的长;②Ⅰ如图2,当BD=BE时,∠BED=∠BDE,故∠BPD=∠BPE=∠BAC根据等角的同名三角函数值相等得出tan∠BPE=2,根据正切函数的定义由AB=2![]() ,得出BP=
,得出BP=![]() , 根据勾股定理即可得出BD=2;Ⅱ如图3,当BE=DE时,∠EBD=∠EDB;由∠APB=∠BDE,∠DBE=∠APC,得出∠APB=∠APC
, 根据勾股定理即可得出BD=2;Ⅱ如图3,当BE=DE时,∠EBD=∠EDB;由∠APB=∠BDE,∠DBE=∠APC,得出∠APB=∠APC
②Ⅰ如图2,当BD=BE时,∠BED=∠BDE, 由等角对等边得出AC=AB= 2![]() , 过点B作BG⊥AC于点G,得四边形BGCD是矩形,根据正切函数的定义得出AG=2,进而得出BD=CG=2
, 过点B作BG⊥AC于点G,得四边形BGCD是矩形,根据正切函数的定义得出AG=2,进而得出BD=CG=2![]() -2,;Ⅲ如图4,当BD=DE时,∠DEB=∠DBE=∠APC ,由∠DEB=∠DPB=∠BAC得出∠APC=∠BAC,设PD=x,则BD=2x,根据正切函数的定义列出关于x的方程,求解得出x的值,进而由BD=2x得出答案;
-2,;Ⅲ如图4,当BD=DE时,∠DEB=∠DBE=∠APC ,由∠DEB=∠DPB=∠BAC得出∠APC=∠BAC,设PD=x,则BD=2x,根据正切函数的定义列出关于x的方程,求解得出x的值,进而由BD=2x得出答案;
(3)如图5,过点O作OH⊥DC于点H,根据tan∠BPD=tan∠MAN=1得出BD=DP,令BD=DP=2a,PC=2b得OH=a,CH=a+2b,AC=4a+2b,由OC∥BE得∠OCH=∠PAC,根据平行线分线段成比例定理得出OH·AC=CH·PC,从而列出方程,求解得出a=b,进而表示出CF,OF,故可得出答案.
详解:
(1)解 :∵PB⊥AM,PC⊥AN
∴∠ABP=∠ACP=90°,
∴∠BAC+∠BPC=180°
∵∠BPD+∠BPC=180°
∴∠BPD=∠BAC
(2)解 ;①如图1,
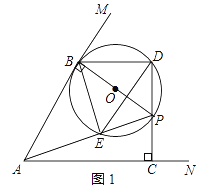
∵∠APB=∠BDE=45°,∠ABP=90°,
∴BP=AB=![]()
∵∠BPD=∠BAC
∴tan∠BPD=tan∠BAC
∴ ![]() =2
=2
∴BP=![]() PD
PD
∴PD=2
∴∠BPD=∠BPE=∠BAC
∴tan∠BPE=2
∵AB=![]()
∴BP=![]()
∴BD=2
Ⅱ如图2,当BE=DE时,∠EBD=∠EDB
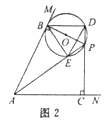
∵∠APB=∠BDE,∠DBE=∠APC
∴∠APB=∠APC
∴AC=AB=2![]()
过点B作BG⊥AC于点G,得四边形BGCD是矩形
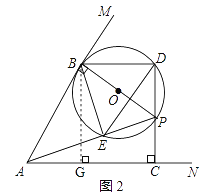
∵AB=![]() ,tan∠BAC=2
,tan∠BAC=2
∴AG=2
∴BD=CG=![]()
Ⅲ如图4,当BD=DE时,∠DEB=∠DBE=∠APC
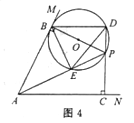
∵∠DEB=∠DPB=∠BAC
∴∠APC=∠BAC
设PD=x,则BD=2x
∴ ![]() =2
=2
∴ ![]() =2
=2
∴x=![]()
∴BD=2x=3
综上所述,当BD为2,3或![]() 时,△BDE为等腰三角形
时,△BDE为等腰三角形
(3)![]() ,
,
如图5,过点O作OH⊥DC于点H
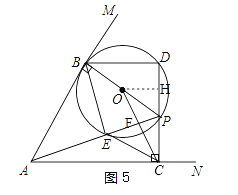
∵tan∠BPD=tan∠MAN=1
∴BD=DP
令BD=DP=2a,PC=2b得
OH=a,CH=a+2b,AC=4a+2b
由OC∥BE得∠OCH=∠PAC
∴ ![]()
∴OH·AC=CH·PC
∴a(4a+2b)=2b(a+2b)
∴a=b
∴CF=![]() ,OF=
,OF= ![]()
∴![]() .
.

【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高.某社区为了了解家庭对于文化教育的消费悄况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调査,根据调查结果绘制成两幅不完整的统计图表.
请你根据统计图表提供的信息,解答下列问题:
组別 | 家庭年文化教育消费金额x(元) | 户数 |
A | x≤5000 | 36 |
B | 5000<x≤10000 | m |
C | 10000<x≤15000 | 27 |
D | 15000<x≤20000 | 15 |
E | x>20000 | 30 |
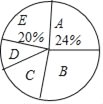
(1)本次被调査的家庭有__________户,表中 m=__________;
(2)本次调查数据的中位数出现在__________组.扇形统计图中,D组所在扇形的圆心角是__________度;
(3)这个社区有2500户家庭,请你估计家庭年文化教育消费10000元以上的家庭有多少户?